Mocninová funkcia je také čudo medzi funkciami, pretože už nebolo názvov na pomenovanie všetkých druhov funkcií, tak boli pomenované všeobecným názvom mocninové. V zásade môžeme kľudne prehlásiť, že mocninovými funkciami sú všetky druhy funkcií, ktoré poznáme a narábajú s čistou hodnotou x.
Ako to myslím? No tak, že funkcie ako sin(x), log(x), e^x nie sú mocninové, lebo s hodnotou x narábajú inak, ako len umocňovaním.
Mocninová funkcia môže byť napr.:
\[y=4\]kde je x vynásobené nulou. Alebo je mocninovou funkciou aj:
\[y=4x+1\]kde je x umocnené na prvú. (Všimni si slovo „umocnené“, odtiaľ názov mocninová.)
No a keď sa trochu pohráme s hodnotou x, môžeme mať ako mocninovú funkciu toto:
\[y=-4x^4+x^3+5x^2-x+1\]Vo všeobecnosti sa dá mocninová funkcia zapísať takto:
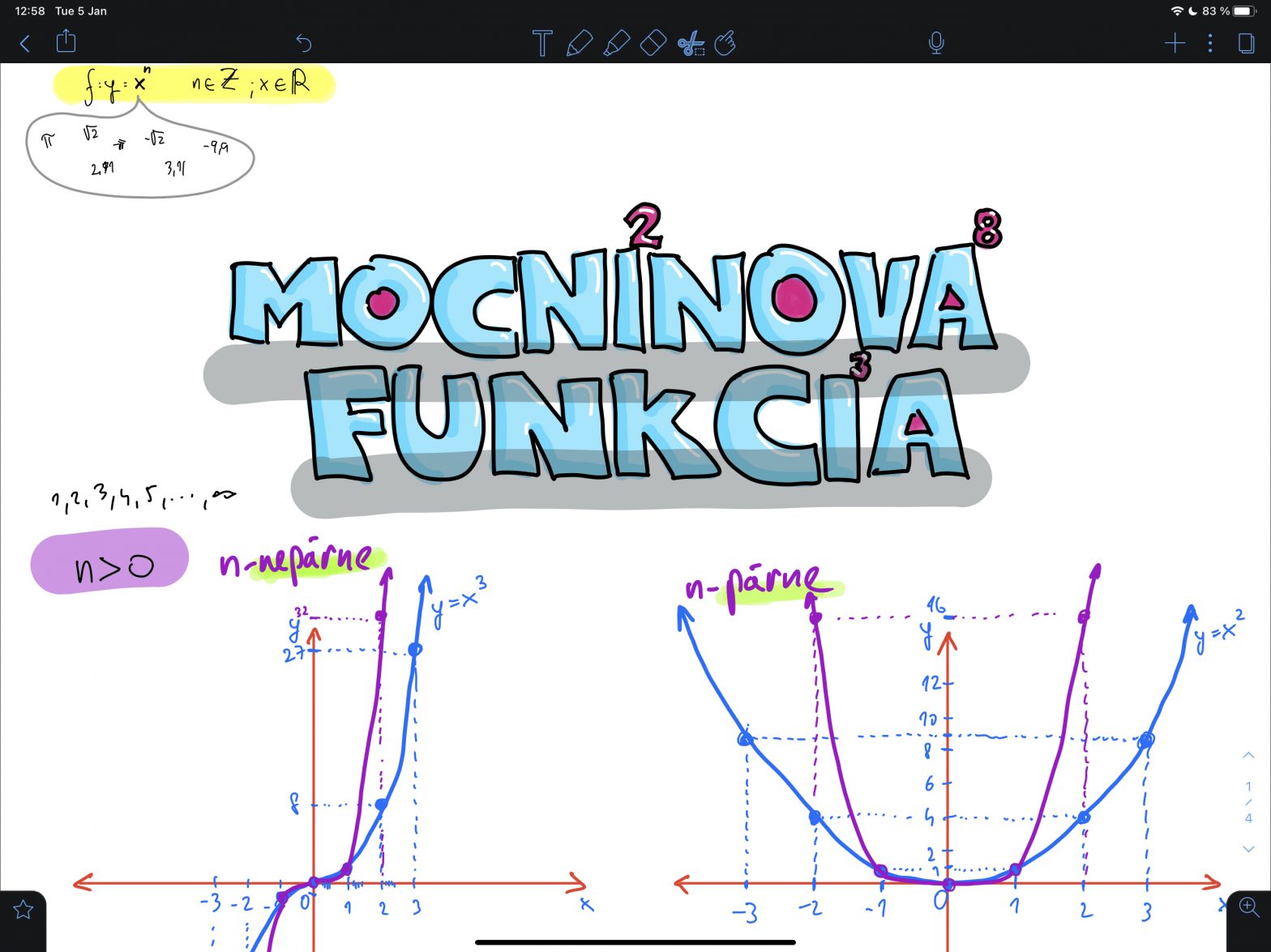
\[y=x^n\]kde je n ľubovoľné celé číslo.
Preto v tejto sérii rozoberám len základné prípady mocninových funkcií, aby sme nemuseli pokračovať do nekonečna a ešte ďalej.
Pridaj komentár