Značka: matika
-
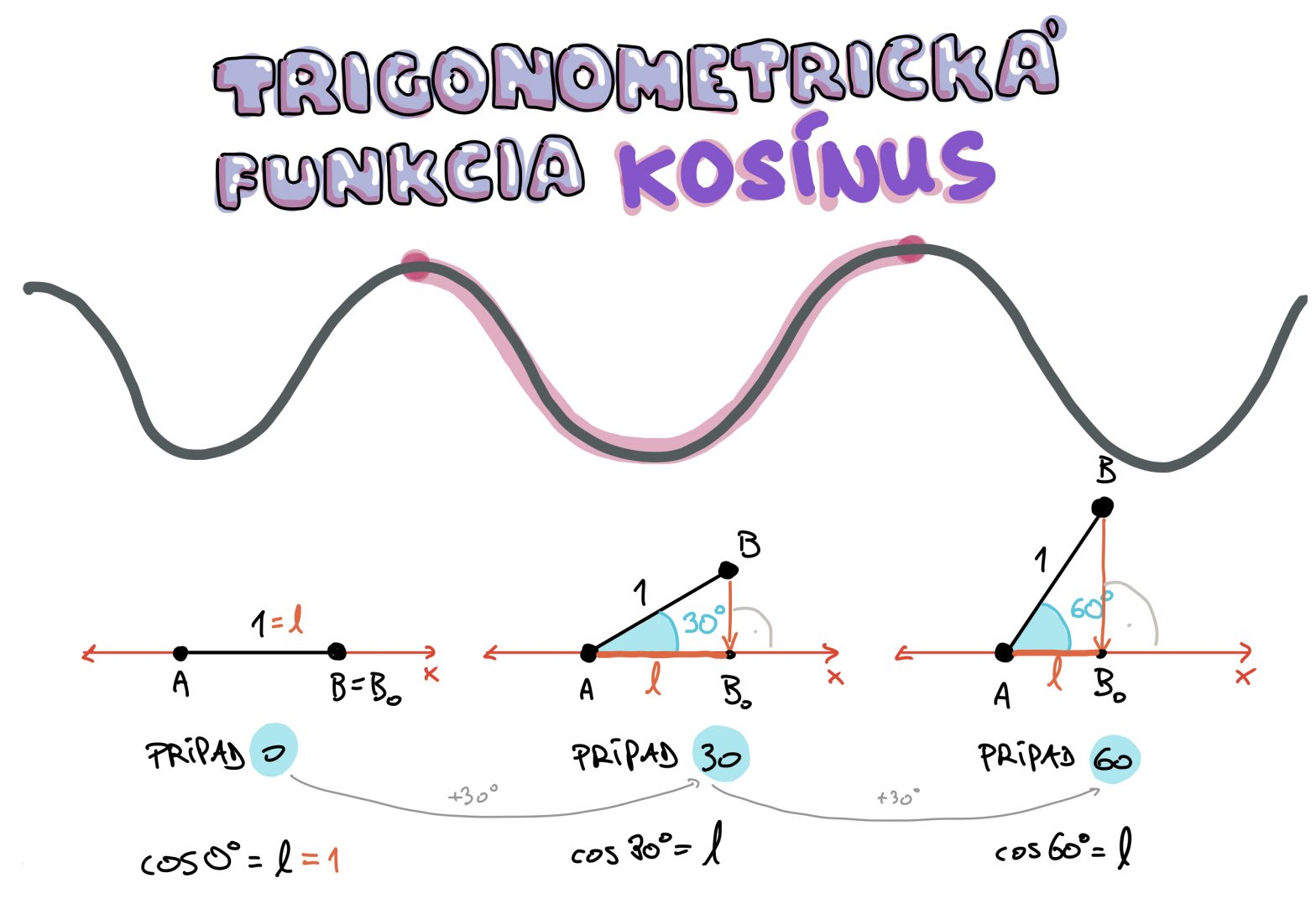
Trigonometrická funkcia kosínus
Kosínus je funkcia, ktorá je súrodencom funkcie sínus. Je k tej prilepená v tesnom závese o pravý uhol. Tak sleduj, a uč sa!
-
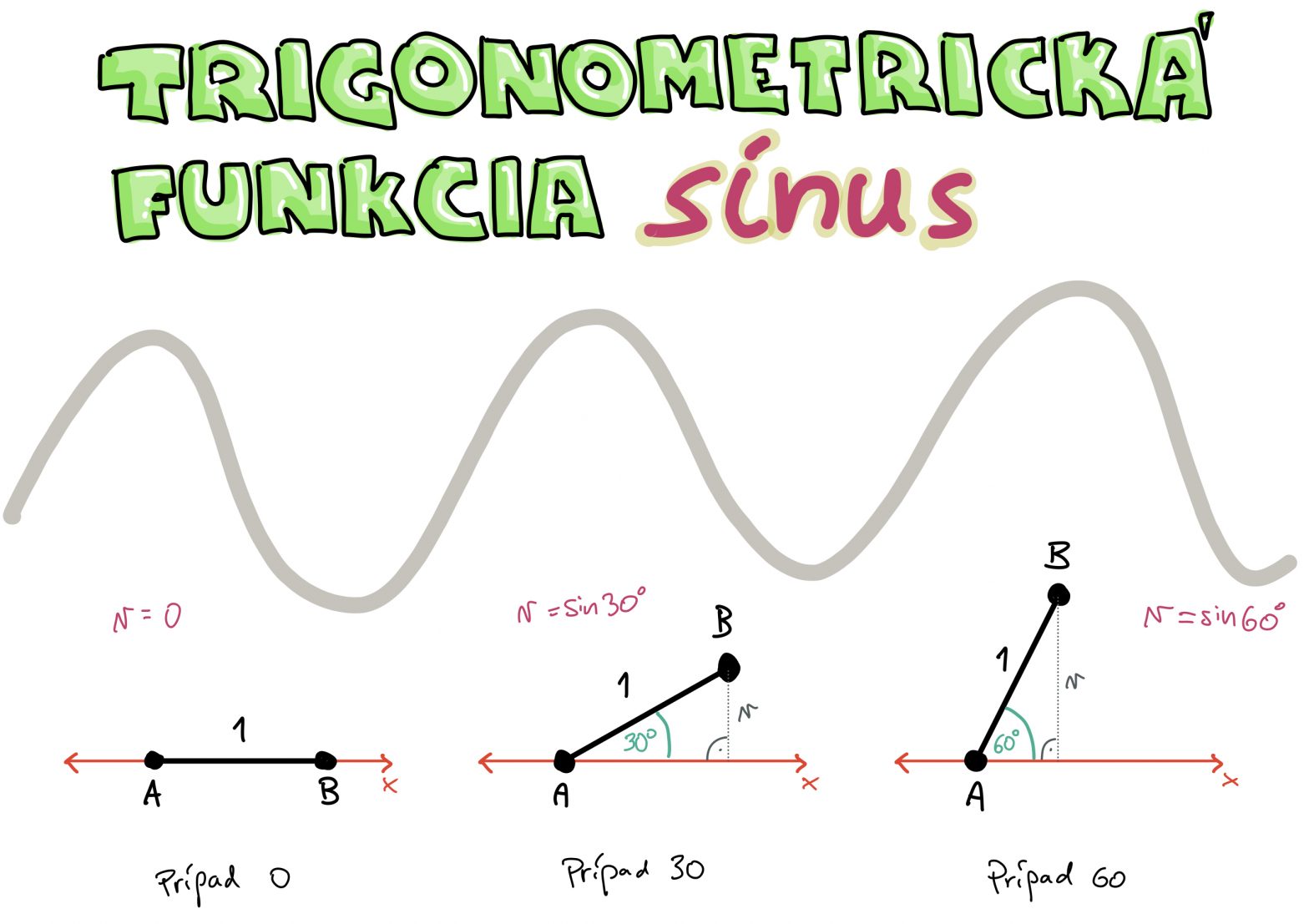
Trigonometrická funkcia sínus
Trigonometrická (niekedy aj goniometrická) funkcia sínus je základ, ako pochopiť meniace sa patterny (vzory) v priestoročase, ktoré úzko súvisia s pravouhlými trojuholníkmi. Tak sleduj, a uč sa!
-
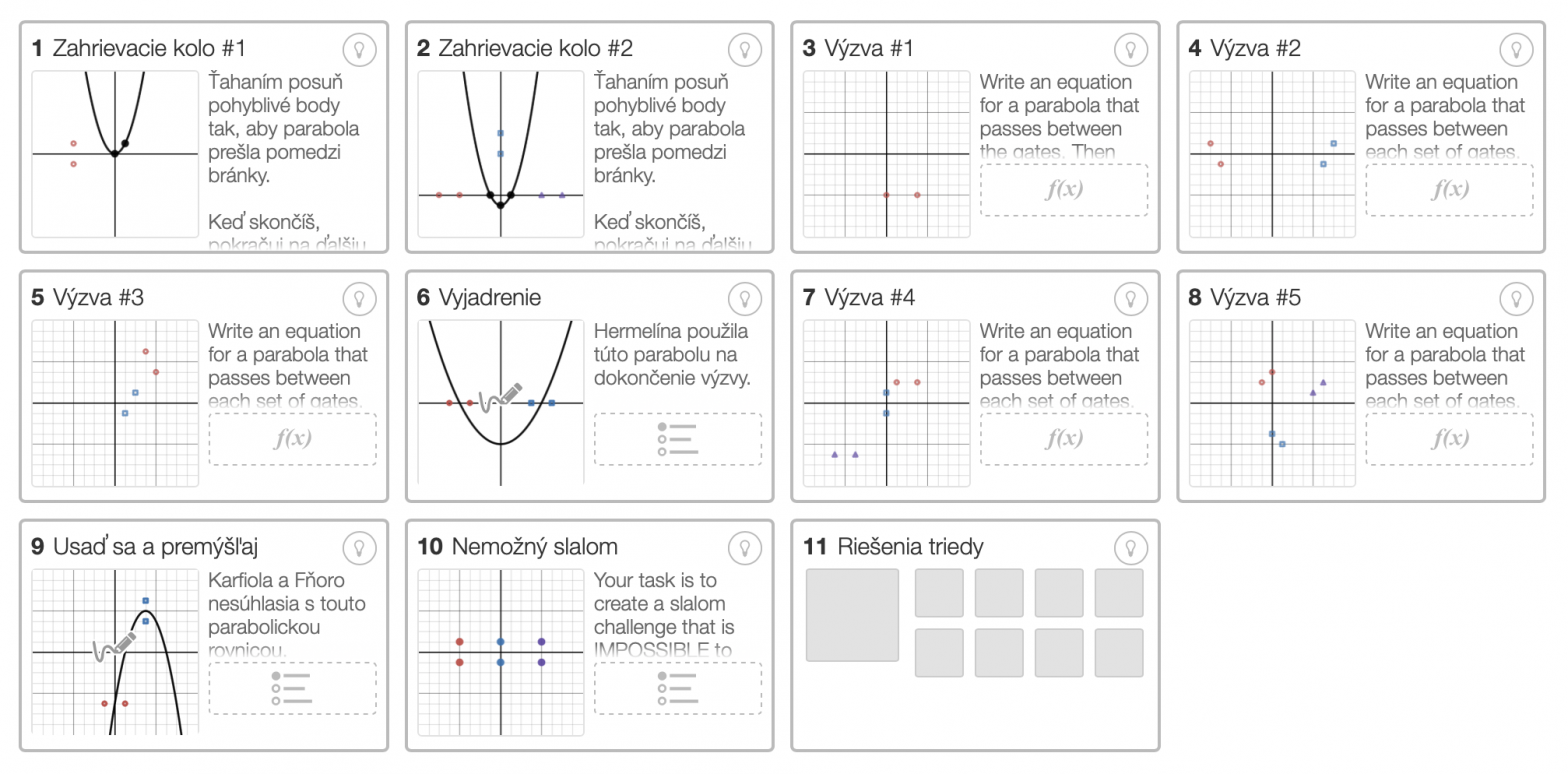
Parabolický slalom
Dynamické narábanie s parabolami je kľúčovou časťou pri pochopení kvadratických funkcií. Čo takto si zahrať hru, pri ktorej musíš trafiť krivku kvadratickej funkcie, teda paraboly, medzi vyznačené bránky? Poď si zahrať parabolický slalom. Tu je odkaz na hru. Každopádne, pre vysvetlenie. Klikni na prvé zahrievacie kolo, čítaj si inštrukcie a skúšaj. Každé kolo je jedna…
-
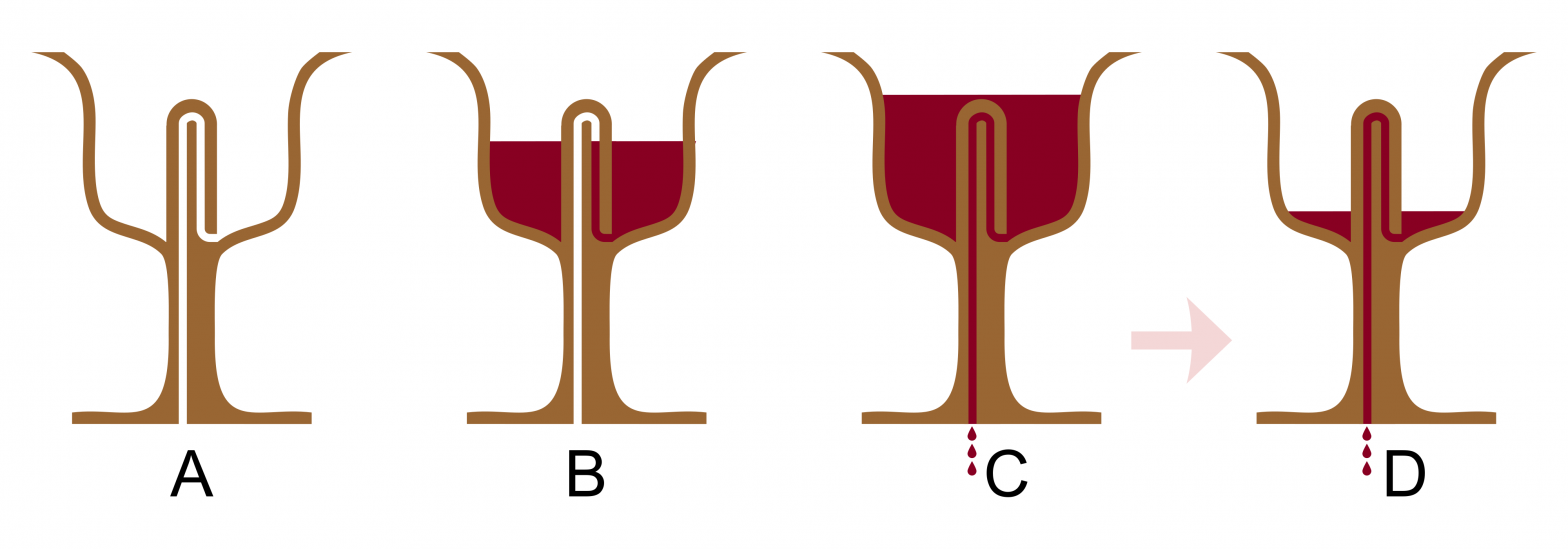
Pytagorejský pohár
Pytagoras je okrem slávnych matematických vzťahov preslávený dômyselným pohárom, ktorým trestal svojich žiakov za chymtivosť, ak si doň naliali viac vína, ako bolo únosné. To bolo ešte v časoch, keď učiteľ so žiakmi mohol piť víno úplne bežne. Obrázok 1 ilustruje 4 stavy. Stav A je prázdny pohár, stav B je pohár naplnený tak, aby…
-

Logaritmická funkcia
Logaritmická zmena nejakého vzoru (patternu) je v zásade spomaľujúca. Čím dlhšie sa na zmenu pozeráš, tým pomalšie sa mení a stále spomaľuje. V tejto sérii videí si môžeš pozrieť, ako získať z pozorovania takej zmeny všeobecný vzorec, nejaké dáta a nakoniec graf. Vlastnosti logaritmickej funkcie z toho všetkého vyplynú samé.
-
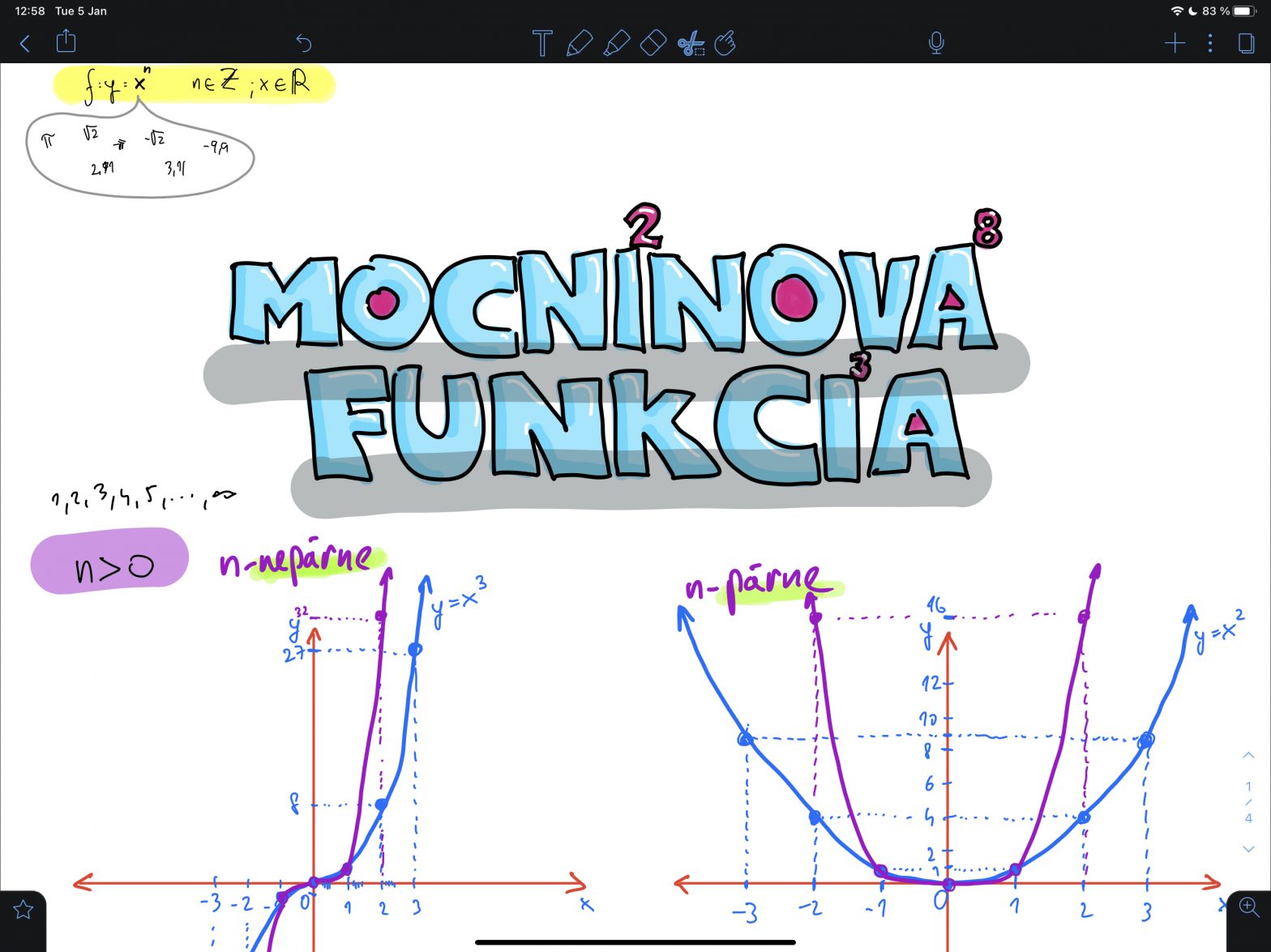
Mocninová funkcia
Mocninová funkcia je také čudo medzi funkciami, pretože už nebolo názvov na pomenovanie všetkých druhov funkcií, tak boli pomenované všeobecným názvom mocninové. V zásade môžeme kľudne prehlásiť, že mocninovými funkciami sú všetky druhy funkcií, ktoré poznáme a narábajú s čistou hodnotou x. Ako to myslím? No tak, že funkcie ako sin(x), log(x), e^x nie sú…
-
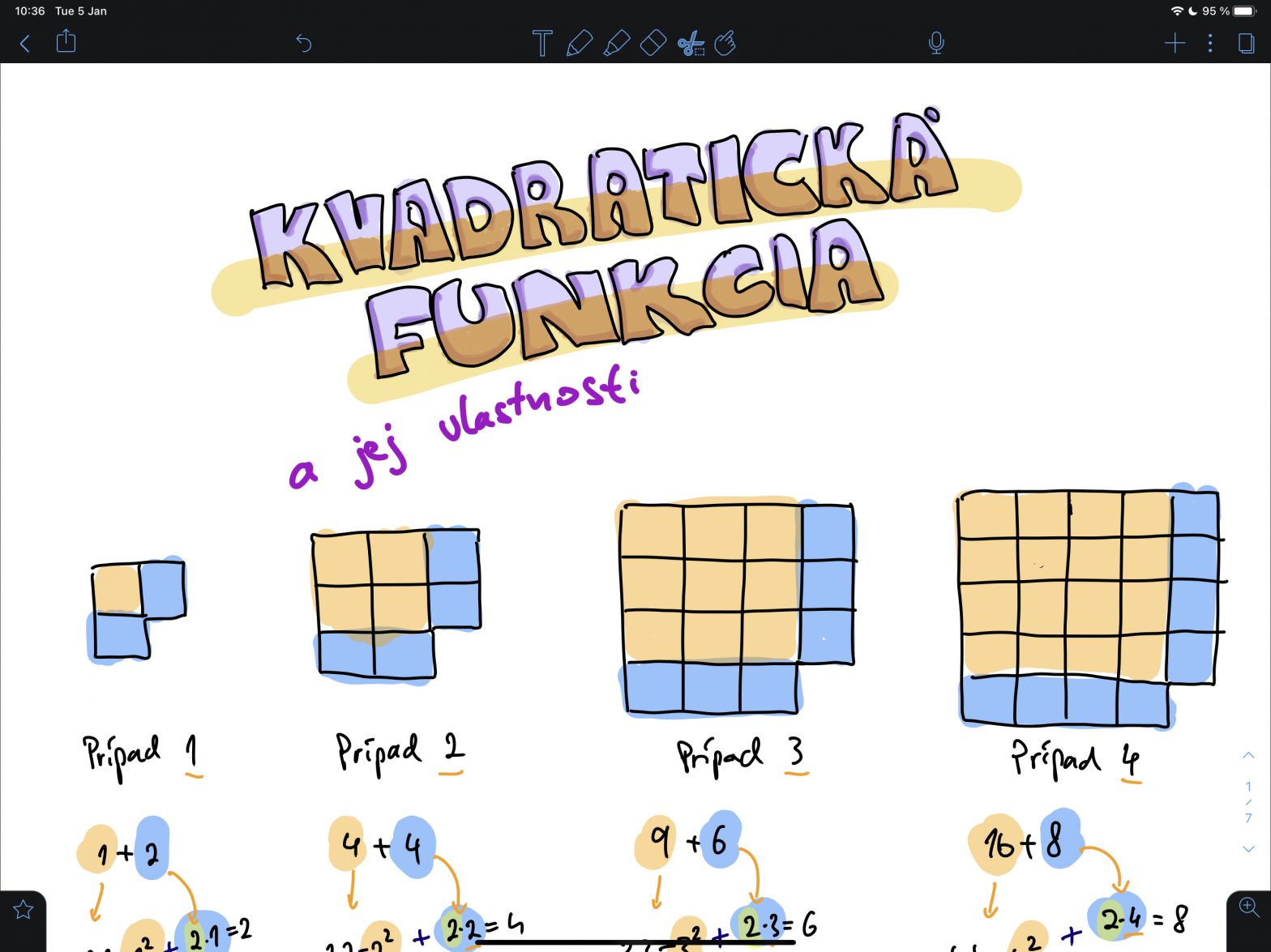
Kvadratická funkcia
Kvadratická funkcia bola popísaná na základe skúmania tvarov, ktoré sa menia s druhou mocninou. Napríklad zmena plochy dačoho. Či už plochy štvorca vzhľadom na dĺžku strany, plochy kruhu vzhľadom na polomer, alebo hodnoty y vzhľadom ku hodnote x^2. V tejto sérii sa pozrieme na pár zaujímavých vlastností kvadratickej funkcie, ako je jej priebeh (bez derivácie),…
-
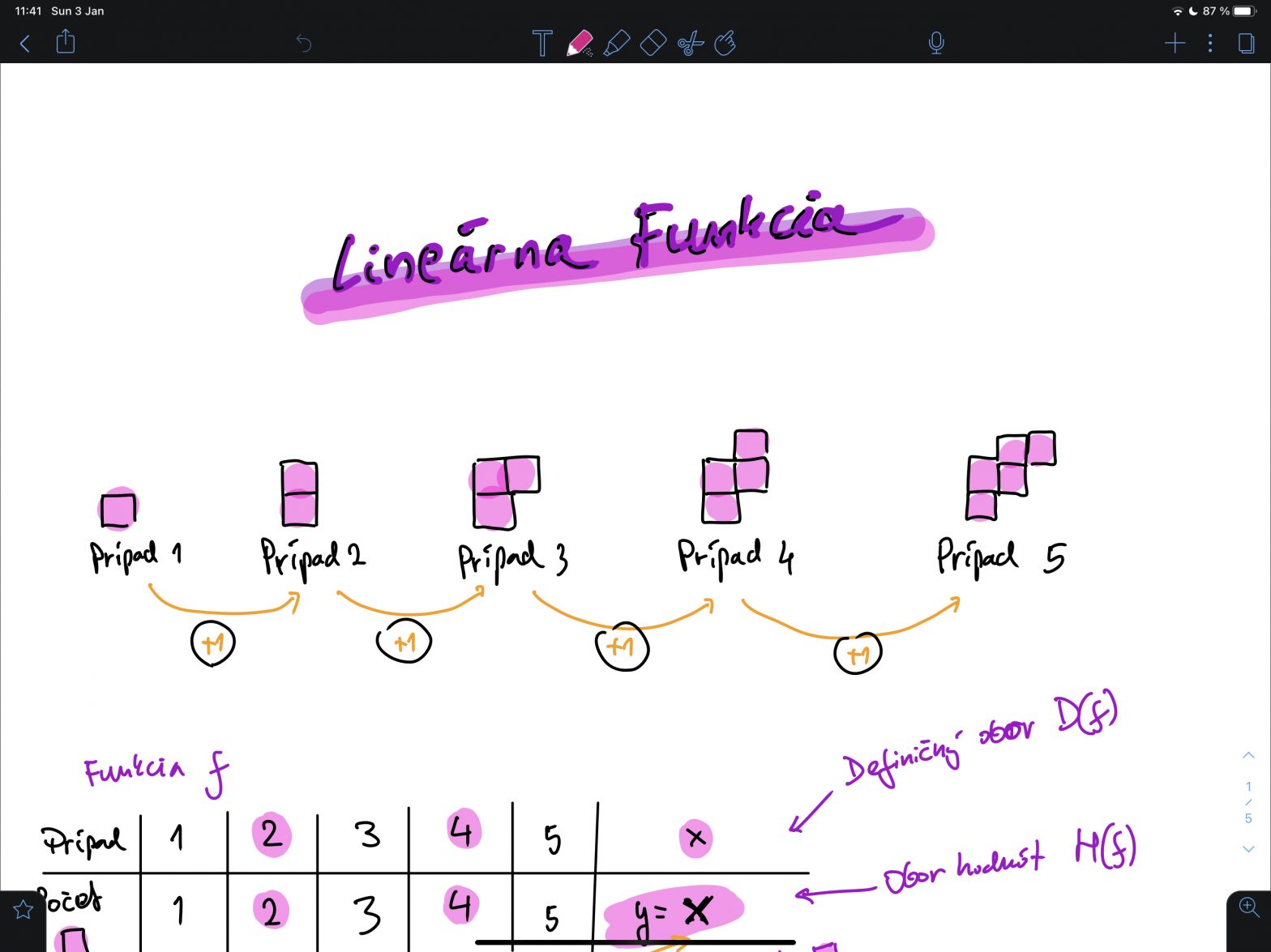
Lineárna funkcia
Na lineárnu funkciu sa pozrieme z pohľadu zmeny tvaru v časopriestore tak, aby bolo zrejmé, ako vzniká vzorec, čo popisuje graf a aké sú jej vlastnosti. Pozrieme sa na zúbok rastúcej, klesajúcej aj konštantnej zmeny tvaru.
-
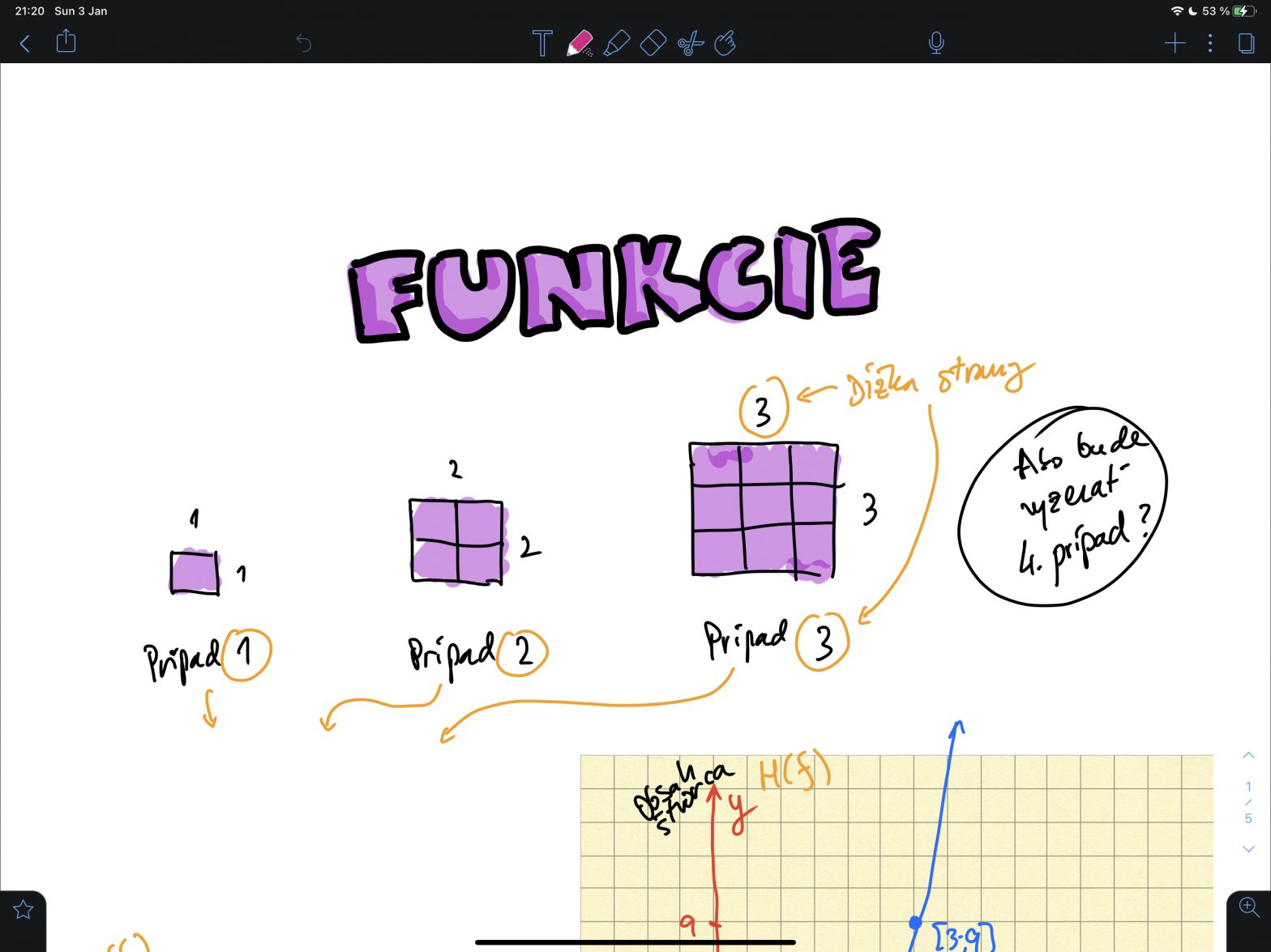
Funkcie – vzťahy v matematike
Funkcia sa dá vyjadriť zmenou tvaru, ktorý sa mení v priestoročase vzhľadom na stavy pozorovateľa. Natočil som o nich sériu popisných videí, tak pokukaj, aby si chápal/a funkcie v zmysle matematiky. Daj mi vedieť, ak pomohlo, do komentár pod konkrétne video, čo bolo pre teba najviac prínosné. Ďakujem ??.
-

Príbeh nuly
Nula mala ťažké detstvo v Európskej matematike, lebo bola úspešne ignorovaná. Zo začiatku, v časoch starovekého Grécka, sme ako ľudia používali čísla ako reprezentáciu geometrických útvarov: dĺžky, obsahy, objemy… a tie nikdy nemohli byť nulové, lebo by neexistovali. Nedávalo zmysel o nich rozprávať a uvažovať. Grécko Akonáhle ľudia uvažovali nad ničotou (nulou), dostávali sa aj…