Keď hovoríme o kompostovaní kvadratického trojčlena, hovoríme, že hľadáme korene kvadratickej funkcie. To sú priesečníky paraboly (tej krivej čiary na obrázku nižšie) s osou x (to je tá vodorovná čiara na obrázku nižšie). Práve tie body pomocou dômyselnej detektívnej práce ideme nájsť.

Tento spôsob totiž nevyžaduje pamätanie si zbytočných vzorcov. V zásade si pri tejto metóde musíš pamätať len podstatu metódy, žiadny zásadný vzorec na pamätanie sa tu nepoužíva.
Poďme na to.
- Ak ideme kvadratický trojčlen kompostovať, väčšinou máme k dispozícii kvadratickú rovnicu zrovnávajúcu inkriminovaný trojčlen s nulou.

- Cieľom tohto pátrania je získať zápis pomocou dvoch zátvoriek. Z nich práve symboly R a S sú korene, ktoré chceme vypočítať, zistiť, vypátrať.

- Hlodavce prišli na to, že tieto dva tvary kvadratickej rovnice vyjadrujú tú istú nulu, preto ich môžeme medzi sebou porovnať.

- Zátvorky na pravej strane prenásobíme medzi sebou buď „metódou čokoláda“ alebo „každý s každým“. Ľavú stranu nedráždime.

- Lineárne členy na pravej strane sčítame.

- Hlodavce si všimli, že členy na pravej a ľavej strane sa nápadne na seba podobajú. Všimni si číslo pri lineárnom člene x, pri kvadratickom člene x^2 i absolútneho člena. Sú zapísané v rovnakej štruktúre.

- Teraz si tie členy poctivo odpíšeme niekam nabok tak, aby sme ich medzi sebou zrovnali pomocou „rovná sa“.

- Hlodavce si teraz všimli, že presne v strede medzi koreňmi je ich priemerná hodnota (R+S)/2. Preto deleno dvomi, lebo od ľubovoľného koreňa je to polovičná vzdialenosť.

- Od tohto priemeru je každý koreň, aj R, aj S, vzdialený o rovnakú hodnotu, nazvime ju z. Len pozor na znamienko, lebo jeden koreň ide od priemeru doľava (mínus), druhý ide doprava (plus).

- Teraz využijeme vyššie vyskúmaný vzťah -8=-(R+S) a dosadíme ho do rovníc koreňov. Na obrázku nižšie to znázorňujú zelené šípky.

- Čísla v koreňových rovniciach upravíme tak, aby boli vzťahy megacool, aby lákali aj hlodavce.

- Trochu skôr sme vyskúmali vzťah 15=R∙S, ten teraz využijeme na ďalšie úvahy.

- V tomto okamihu ponecháme hlodavce pomiešať daný vzťah s koreňovými rovnicami.

- Získame novú rovnicu, ktorú ideme vyriešiť.

- Pravú stranu upravíme podľa známeho algebraického pravidla (a-b)∙(a+b)=a^2-b^2.

- Teraz musíme urobiť takú vec, že z–ko osamostatníme na pravej strane:
- Na prvom a druhom riadku odpočítame číslo 16 od oboch strán rovnice, aby sme osamostatnili z–ko na pravej strane.
- Na treťom riadku rovnicu prenásobíme mínus jednotkou, aby sme sa zbavili znamienka pri z–ku.
- Výsledkom je rovnica, kde ostáva samostatné kladné z–ko umocnené na druhú, ktoré nadobúda hodnotu 1.

- Výslednú rovnicu 1=z^2 odmocníme, aby sme sa zbavili druhej mocniny nad z–kom.

- Druhá odmocnina má takú vlastnosť, že ak zbavuje druhej mocniny nad z–kom, tak musíme k jednotke na druhej strane pridať znamienka PLUS aj MÍNUS.

- Čiže z sa bude rovnať +1 aj -1.

- Tu sa hlodavce zamyslia a zisťujú, že toto z je opäť možné použiť v koreňových rovniciach, ktoré sme odhalili skôr. Do úvahy vezmeme plusové z, pretože sa jedná o vzdialenosť. V našom svete a vo svete hlodavcov je vzdialenosť vždy plusová. Preto.

- Trochu počítania dá výsledné korene 3 a 5.

- Keď dáme do rovnosti pôvodný kvadratický výraz a výraz v koreňovom tvare, získame novú rovnicu, ktorá je platná, lebo všetky úpravy, čo sme urobili predtým, sú ekvivalentné a matematicky správne.

- Hlodavce, ako aj my ľudia, chcú vedieť, čo to tie korene sú zač. Nakreslíme jeden obrázok, z ktorého je vidno, že korene sú miesta, kde parabola pretína os x. Ak nevieš, ako nakresliť parabolu, tak si urob tabuľku, kde budú x–ové čísla v prvom riadku a v druhom budú hodnoty skúmaného trojčlena po dosadení príslušného z čísel x doňho.

- Stĺpiky uvednej tabuľky sú body paraboly. Tie si do súradnicovej sústavy poznač a spoj ich medzi sebou. Vzniká tak parabola, alebo aj graf kvadratickej funkcie, na ktorej ležia body [-1; 25], [0; 15], [1; 8], [2; 3], [3; 0] – koren 1, [4; -1], [5; 0] – koren 2, [6; 3] atď.

Čím viac týchto bodov spravíš vedľa seba, tým presnejšia bude parabola (graf kvadratickej funkcie). Skús do tabuľky i grafu pridať aj desatinné čísla.
Tento spôsob, ktorý sme si spoločne prešli, je nový spôsob riešenia kvadratickej rovnice, ktorý bol skompletizovaný a uverejnený na konci roku 2019. S viac príkladmi je popísaný aj tu. Objaviteľ tejto metódy ju opisuje aj vo videu:
Ešte existuje jeden všeobecne použiteľný, oveľa starší a viac komplikovaný spôsob riešenia kvadratickej rovnice, pomocou diskriminantu.
Vyskúšaj sa
Je čas na sebavyskúšanie. Pozor! Rozlišuj medzi kvadratickou rovnicou (rovná sa nejakému konkrétnemu číslu) a kvadratickou funkciou (popisuje parabolu).
Rovnice
Kompostuj (rozlož a zisti korene pre) tieto kvadratické rovnice:
\[x^2+7x+12=0\] \[x^2-10x+25=0\] \[\frac{n(n+1)}{2}=0\]Funkcie
Zisti korene kvadratických funkcií. (Čo s tou päťkou pri kvadratickom člene?)
\[f(x)=5x^2+6x+1\]Zisti korene kvadratických funkcií. (Pri kvadratickom člene je jednotka.)
\[f(x)=x^2-x-3\] \[f(x)=x^2-16\]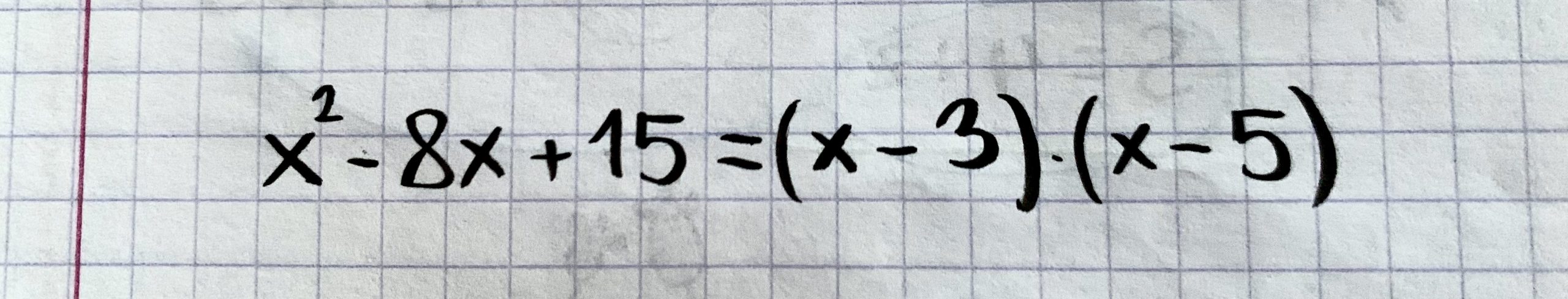
Pridaj komentár