Premena štvorca na štvorec

Alebo ako zistiť z predpisu kvadratickej funkcie, rovnice a čohokoľvek kvadratického vrchol paraboly. Inak povedané, ideme hľadať vrcholový tvar kvadratickej rovnice metódou doplnenia na štvorec.

Ideme rovno na vec, ber to ako návod bez balastu.

1. Majme úplne nudnú kvadratickú rovnicu v najnudnejšom tvare, aký existuje. Existujú aj viac sexy tvary, ale človek musí byť trpezlivý. Všetko má svoj čas.

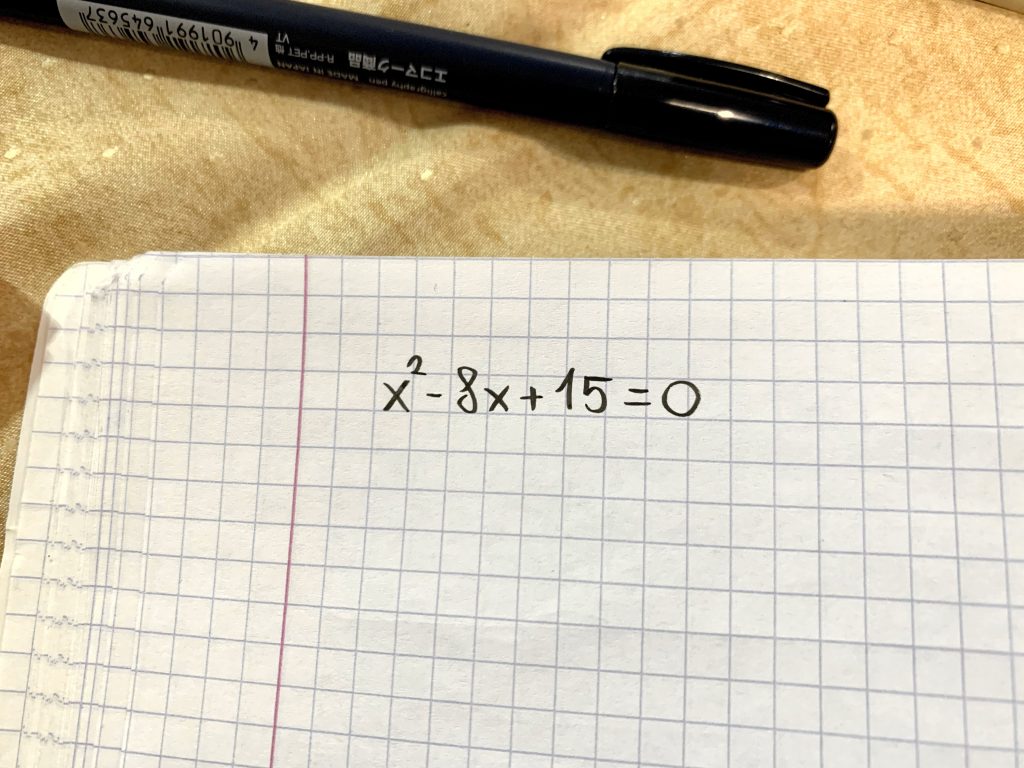
2. Jej ľavú stranu vieme nakresliť ako obsah štvorcov a obdĺžnikov. Toto je stará známa metóda čokoláda.

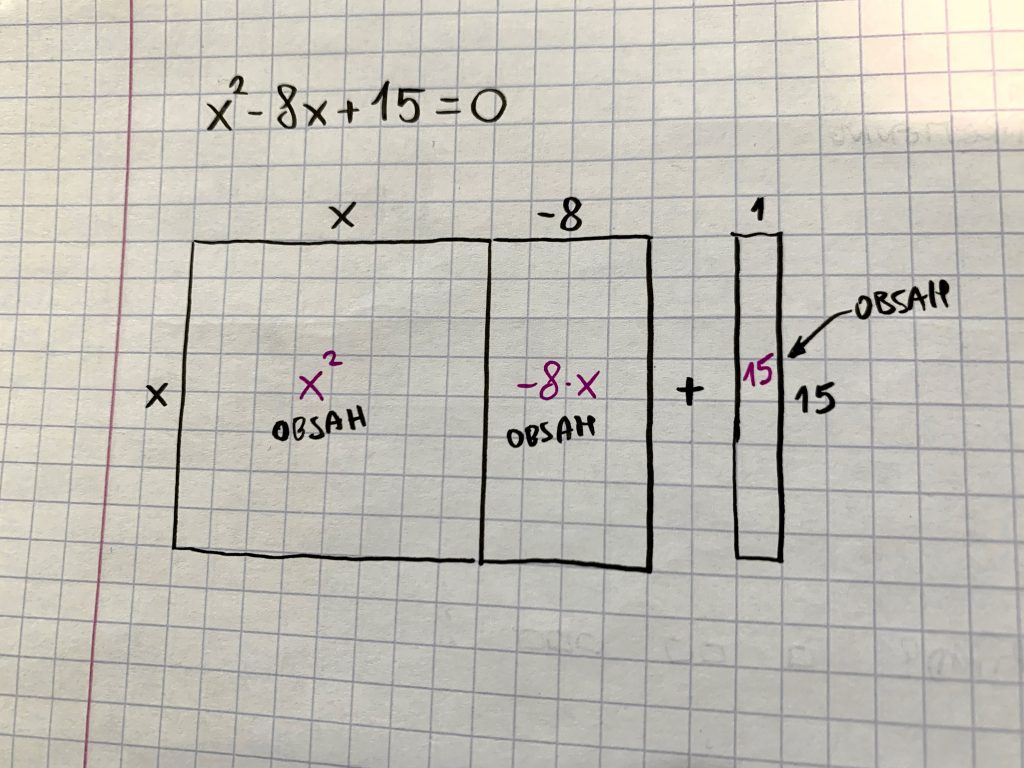
3. Štvorec x na druhú necháme na pokoji. Hovorí sa, že nedráždi kvadratický člen bosou nohou! Rovnako nedráždime žiadnou matematickou operáciou ani absolútny číselný člen. Na polovice rozdelíme len lineárny člen skrze jeho číslo.

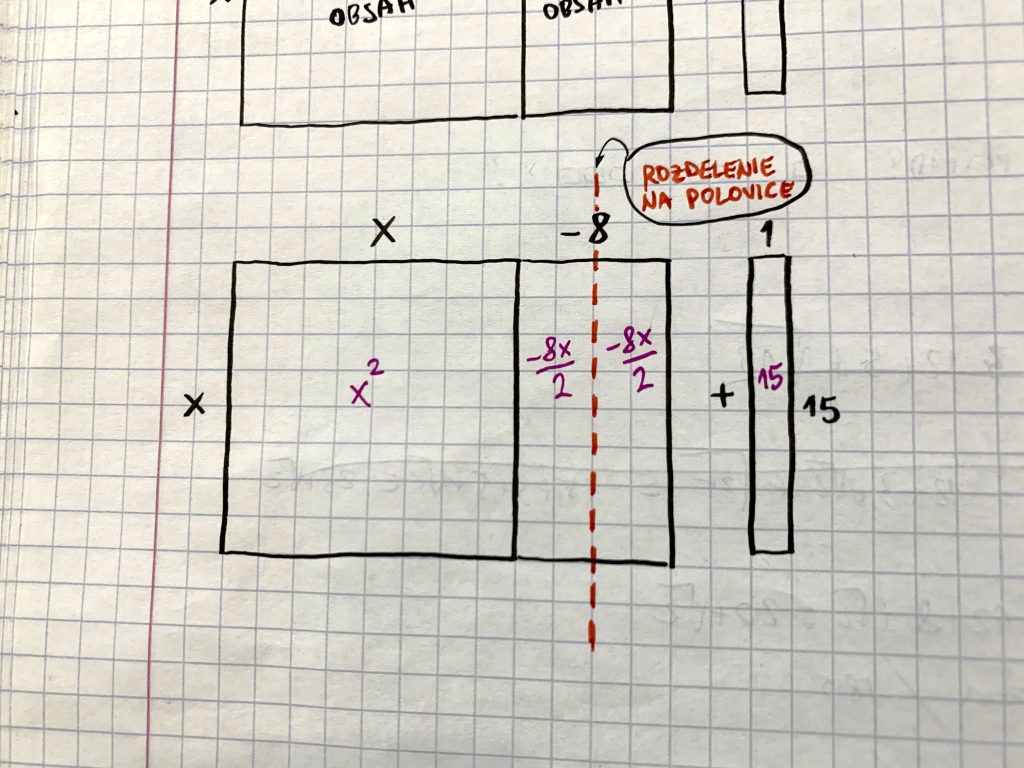
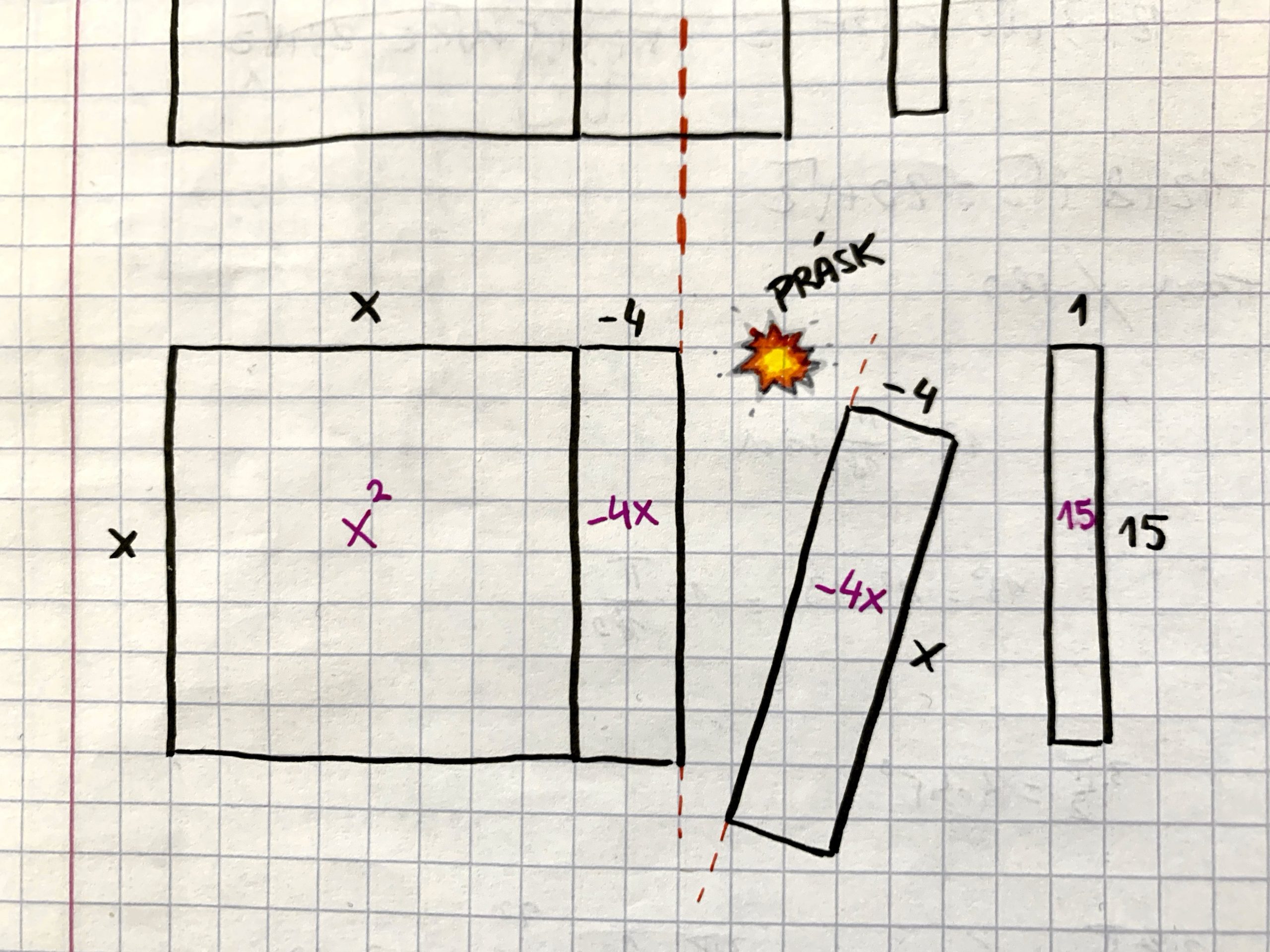
4. PRÁSK!

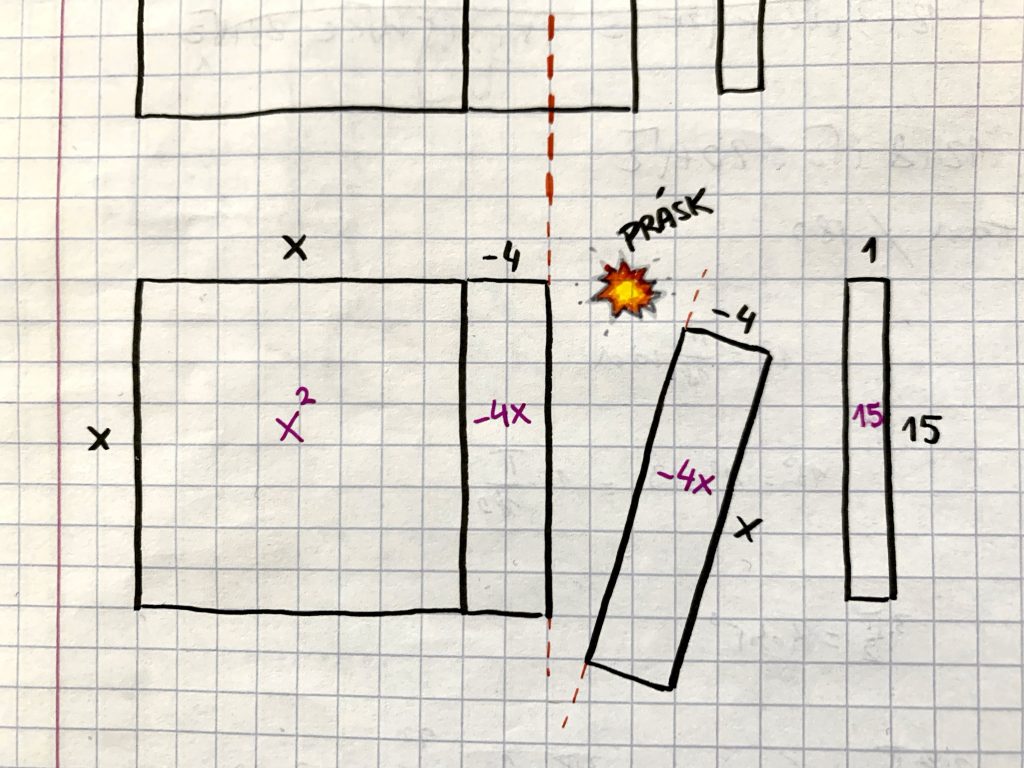
5. Rozdelené lineárne polovičky majú jednu stranu dlhú presne a len presne x. Preto jednu z nich prilepíme zospodu štvorca, ktorý má celkom náhodou tiež stranu dlhú x.

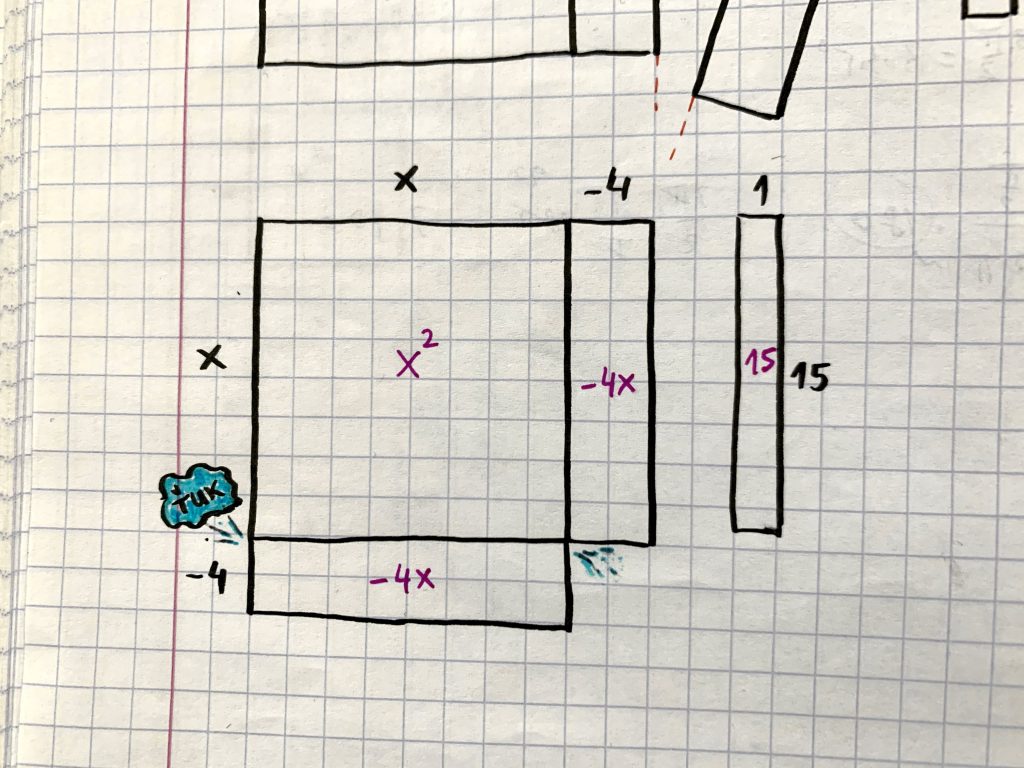
6. Novému štvorcu, ktorý takto vznikol, chýba malý rožtek, ktorý je čírou náhodou v tvare malého štvorca. Dĺžka jeho strany je celkom zrejmá na základe nasilu rozdelených lineárnych polovičiek.
7. Tento nový štvorček pridáme do obrázku, ale aby bolo všetko vo vesmíre v rovnováhe, musíme ho zároveň aj odobrať. Tento trik sa nazýva operácia nula, alebo staré matere zvyknú hovorievať aj operácia nič.

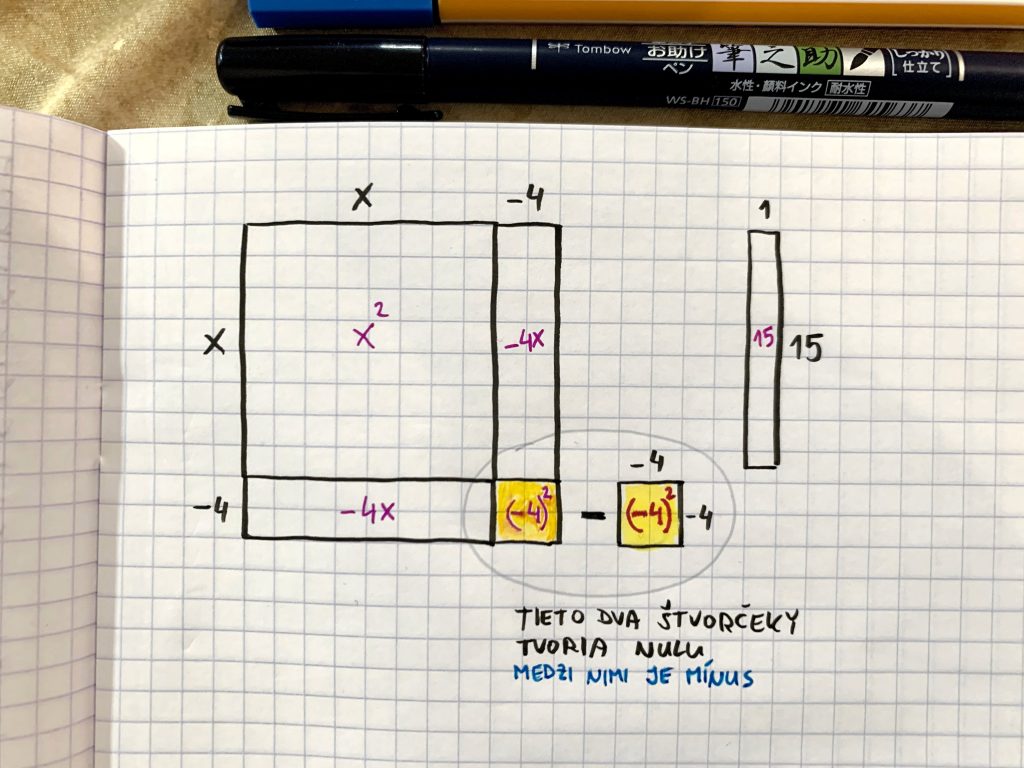
8. A teraz to pomiešame a vyvodíme závery. Uvažuj nad tým, prečo je strana nového štvorca dlhá x – 4.

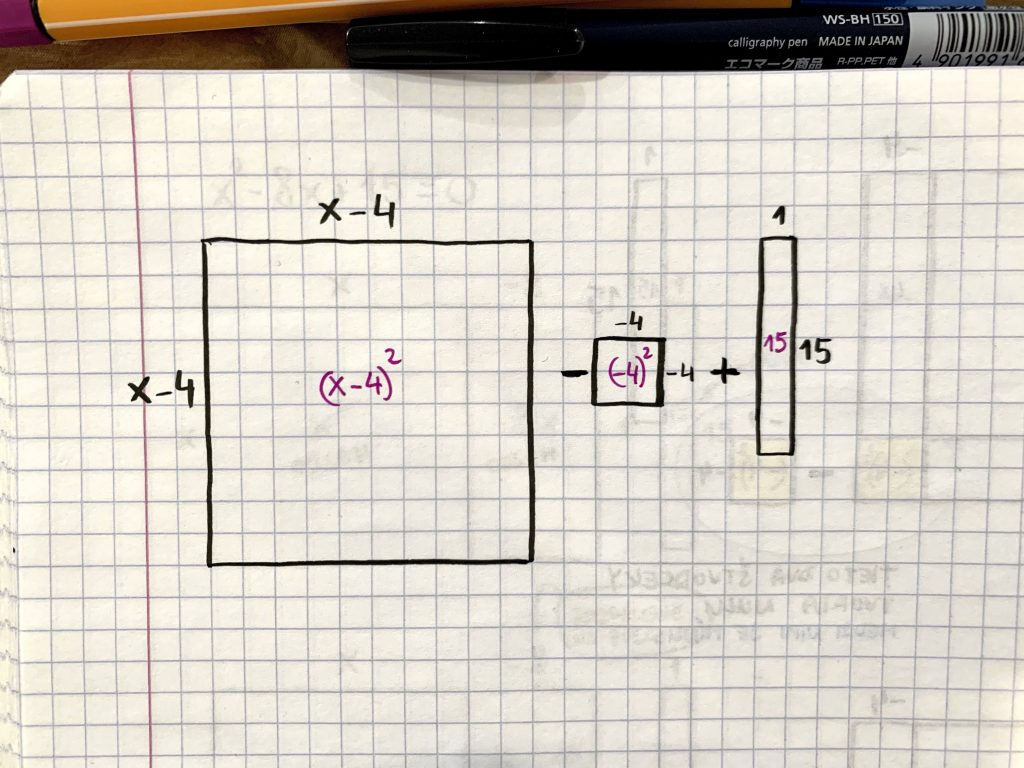
9. Obsahy jednotlivých štvorcov a obdĺžnikov teraz odpíšeme sucho matematicky, znovu navrátime rovnosť a na pravú stranu dáme nulu. Pozor však na znamienka! Fakt bacha na znamienka!

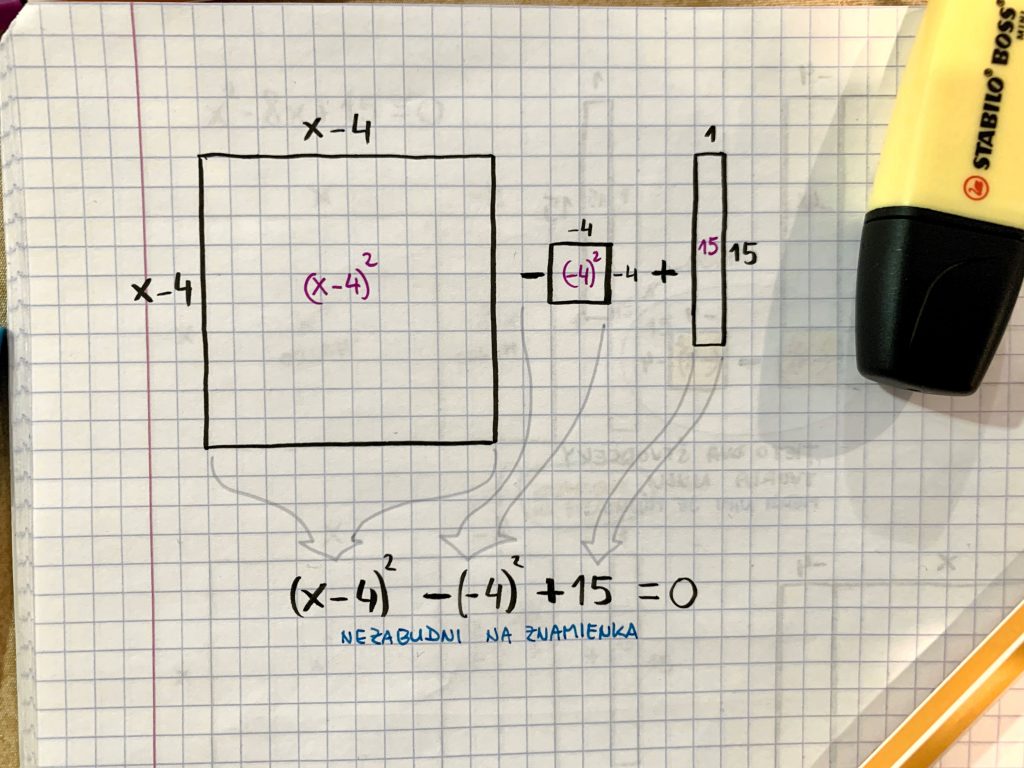
10. Rozpíšeme a spočítame, čo sa spočítať dá. Hlavne tie absolútne čísla, ktoré sa v celej rovnici potuľujú tak trochu nesmelo. Kvadratický člen nechajme na pokoji! 

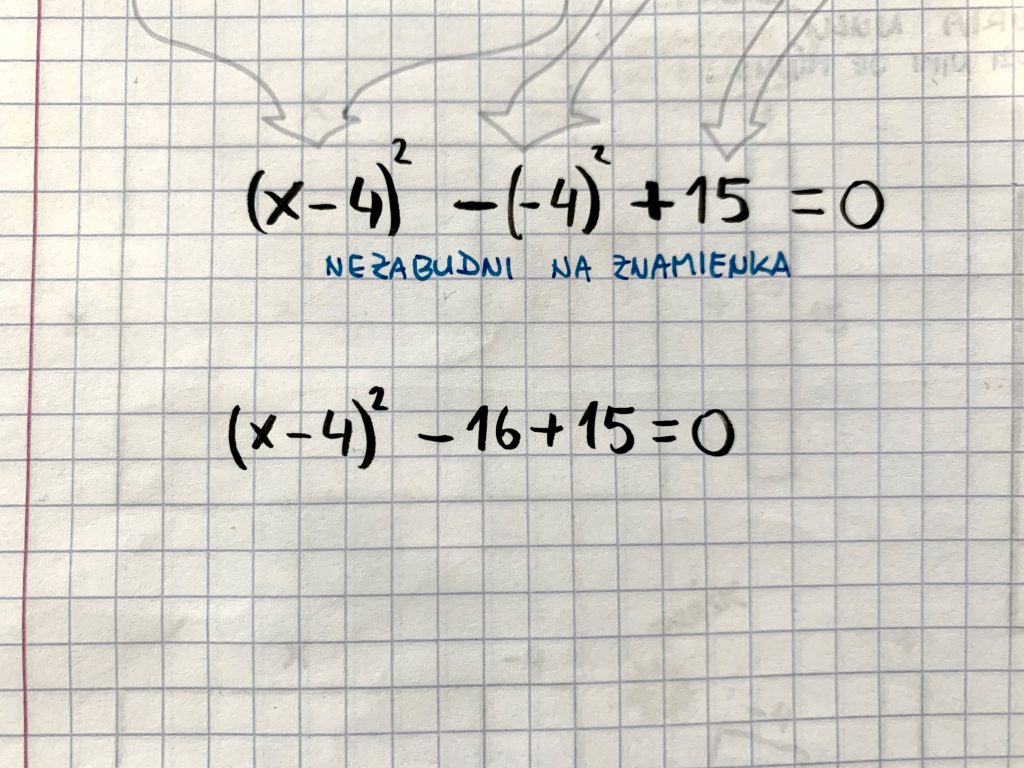
11. Tadá!

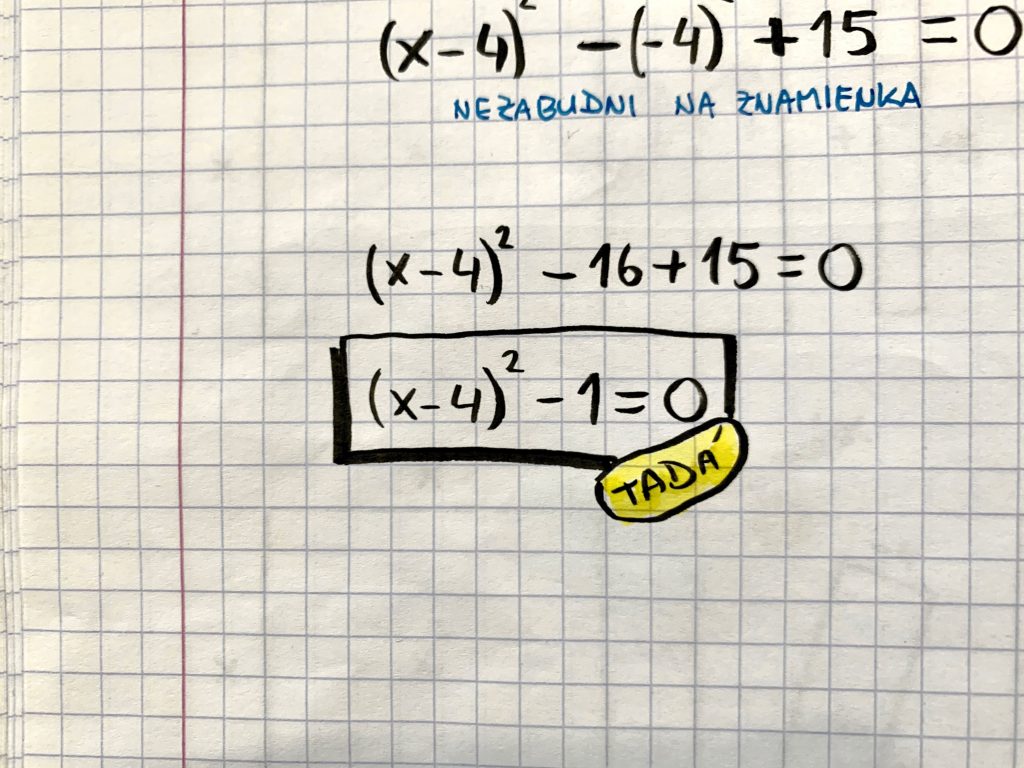
Čo však s tým? Čo to znamená? Na čo je to dobré? Totiž, zistili sme vrchol paraboly. Úplne bez vzorca, čisto iba kreslením, uvažovaním nad obsahmi, presúvaním a sčítaním pár čísel.

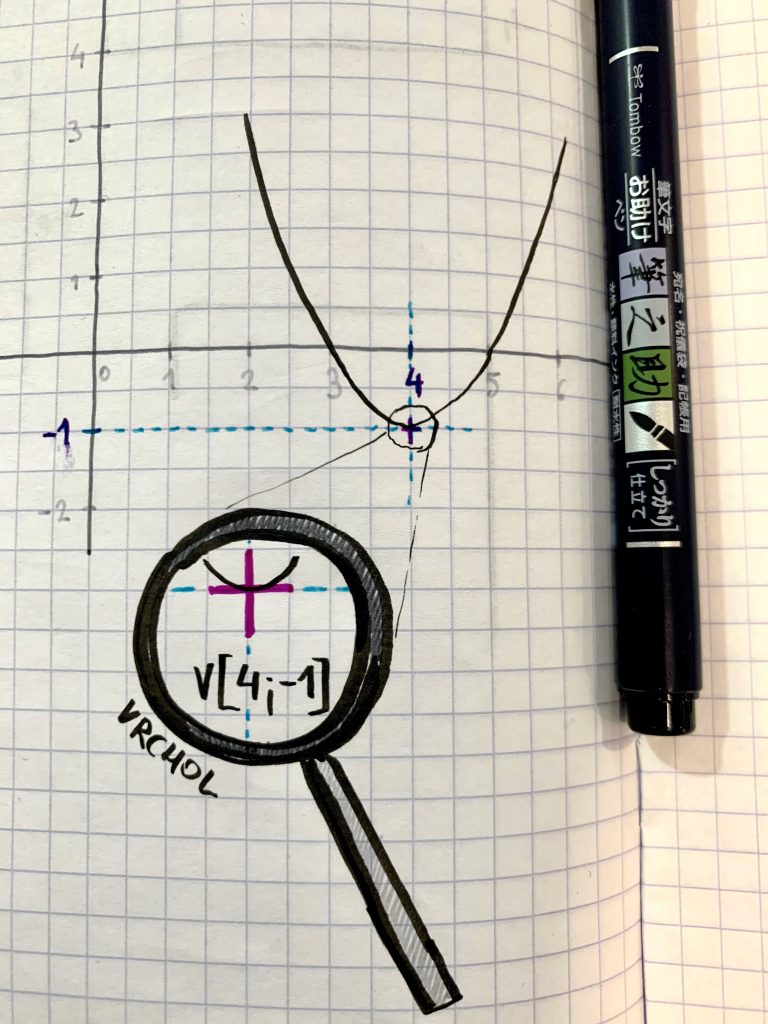
Špeciálne si všimni čísla 4 a 1 v rovnici a zamysli sa nad tým, čo vidíš na obrázku nižšie v grafe.

Precvič si to

Tvojou úlohou je zistiť vrchol každej z týchto parabol.

\[f(x) = x^2-6x+7\] \[f(x) = x^2+4x+7\] \[f(x) = 2x^2-12x+14\]

Svoje výsledky si over pomocou softvéru typu GeoGebra Graphing Calculator alebo Photomath. Teraz vieš metódu doplnenia na štvorec bez nutnosti poznať vzorec.