Čokoláda nie je len chutná, ale aj užitočná vec. Priprav si chuťové poháriky, ideme si prezradiť zákutia matematického vesmíru, o ktorých ti nikto nechce povedať, pretože si chce ušetriť čokoládu pre seba. Dámi a páni, toto je metóda čokoláda.
Prečo je násobenie cool
Násobenie je cool, pretože porušuje intuitívnosť. V škole každého z nás učili, že nemôžeme dávať dokopy hrušky s jablkami. Násobenie to dovoľuje. Dovoľuje, aby ste medzi sebou vynásobili dve čísla, číslo s písmenkom, písmenká medzi sebou, objem s obsahom, škrečka s krokodílom. Sleduj:

Násobenie škrečka s krokodílom neodporúčam, ak nechceš prísť o škrečka. Ako je ale možné násobiť obsah s objemom? Dá sa to povedať aj tak, že máme toľkokrát objem telesa, aký má druhý tvar obsah.
Preto je násobenie cool. A nielen to. O chvíľu zistíš, prečo kvôli násobeniu môžeš pribrať. Tak bacha na postavu.
Budem stále hovoriť o dvoch číslach násobených medzi sebou. Čisto iba pre jednoduchosť. Ak násobíš tri a viac čísel dokopy, rozdeľ si to na postupné násobenie najskôr dvoch a potom výsledku násobenia zo zvyškom, teda zase dvoch čísel. A tak ďalej.
Dve jednociferné čísla
Prichádza čokoláda. Tramtadadá!
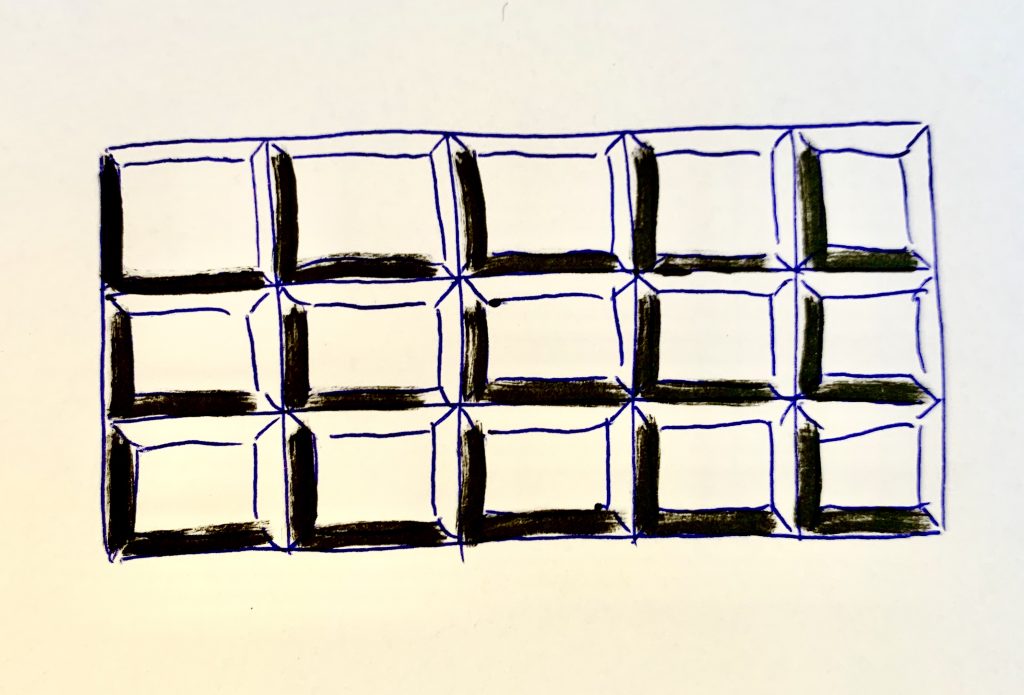
Keď sa opýtam, koľko tabličiek má čokoláda, každý pozná odpoveď aj výpočet. Tri riadky po päť stĺpcov tvorí spolu pätnásť tabličiek. Za podmienky, že čokoládu nenašiel iný rodinný príslušník alebo škrečok za predpokladu, že ho nezjedol krokodíl.
Zápis je 3*5=15.
Pomocou čokolády vieš vynásobiť akékoľvek dve jednociferné čísla.
Dve viacciferné čísla
Keď ti však dám vypočítať 99*97, asi bude dosť namáhavé kresliť čokoládu s 99 stĺpcami a 97 riadkami. Nedávalo by to zmysel a rozhodne by si aj moc rýchlo vypísal pero, čo nechceš, pretože o pár minút to môže byť životne dôležité. Ani spočítať počet tabličiek takej mega čokolády nie je triviálne.
Aj napriek tomu čokoládu nakreslíme. Bude mať však toľko tabličiek, koľko je cifier v oboch číslach. Kuk sem:
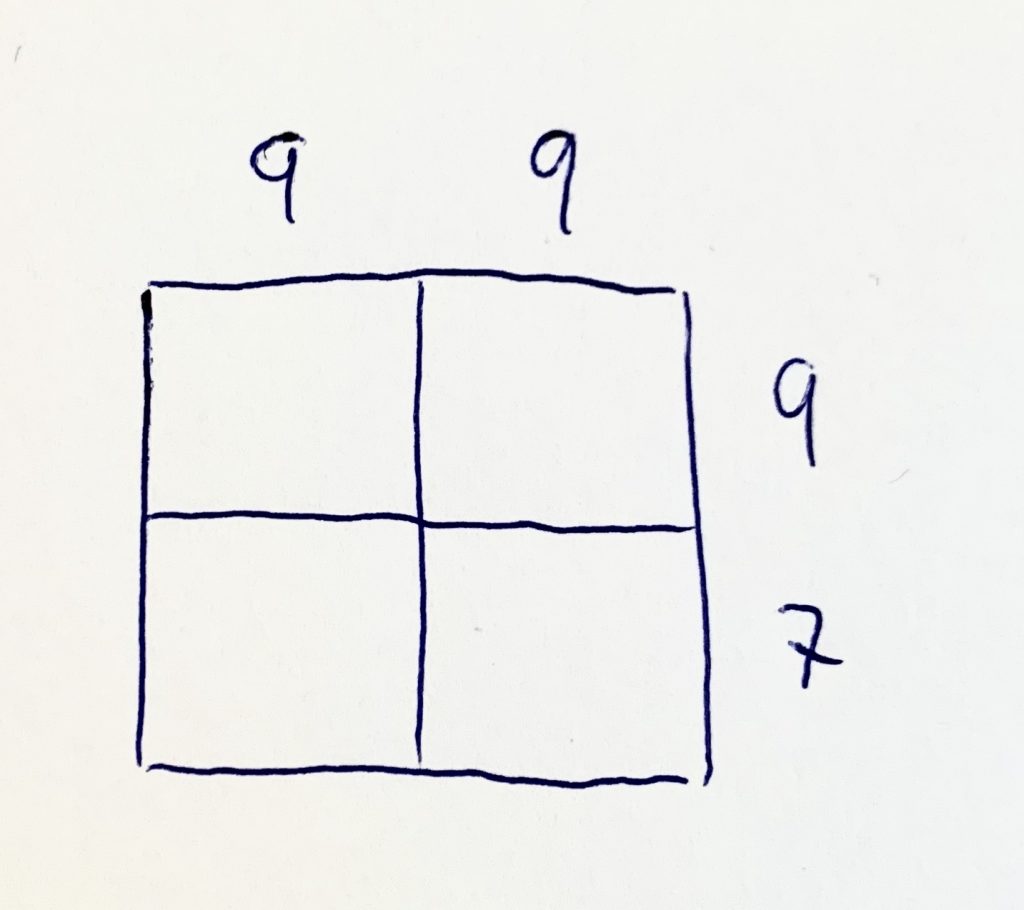
Ak dostaneš dve trojciferné čisla, tak čokoláda bude mať 3 krát 3 tabličky. Všimni si, že po stranách čokolády som napísal dané čísla, ktoré idem vynásobiť.
Teraz čokoládu rozrež dosť ostrým nožom (pozor na zranenia) podľa diagonál jednotlivých tabličiek:
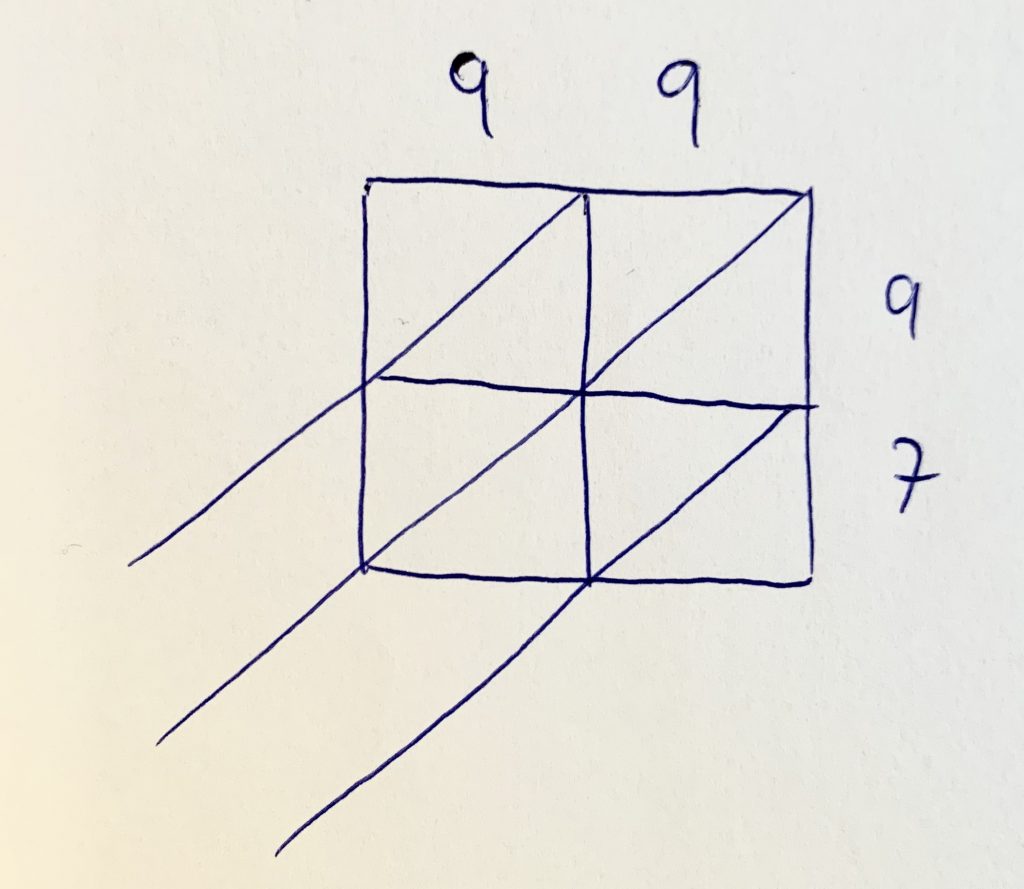
Každá tablička čokolády bude teraz menšou miničokoládkou, ktorá bude mať toľko tabličiek, ako je násobok čísel po jej stranách. Takže postupne máme deväť krát deväť, deväť krát deväť, deväť krát sedem a deväť krát sedem. Kukni a rozmýšľaj, prečo sú zapísané tak zvláštne:
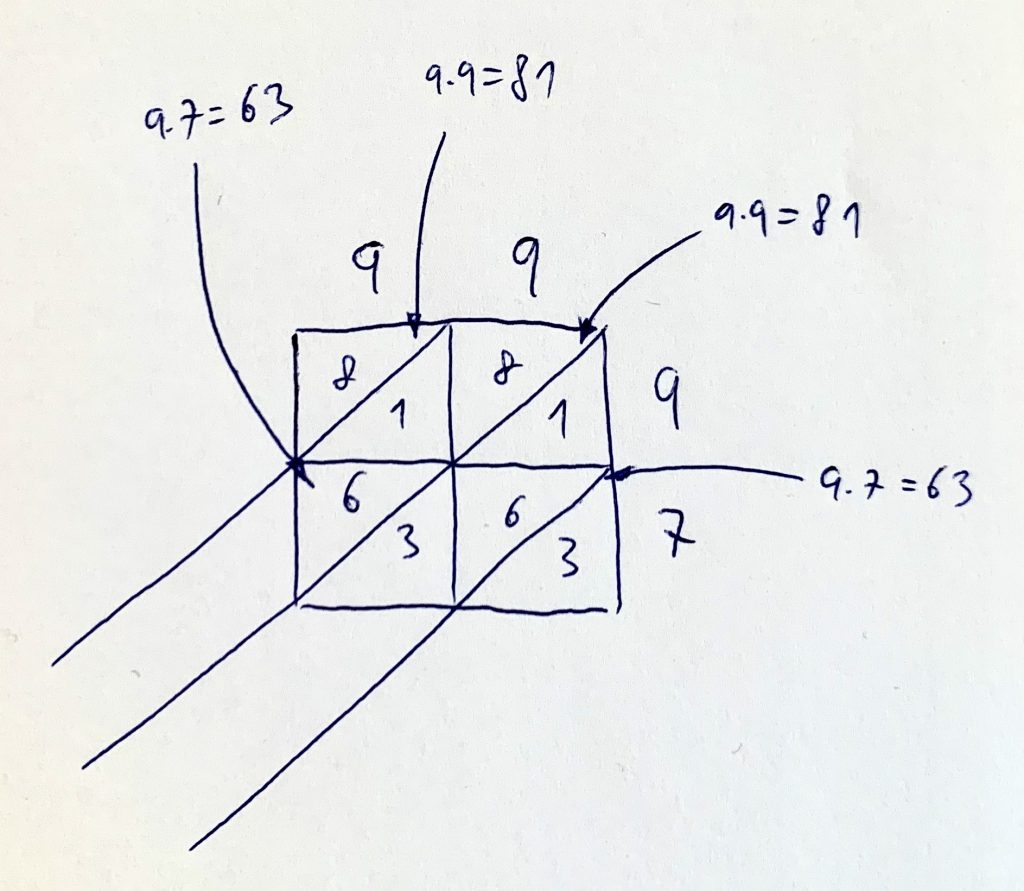
Namiesto kreslenia minitabličiek do tabličiek veľkej čokolády napíšeme číslo tak, že jeho cifry budú rozdelené diagonálnymi rezmi. (Takto nakrájaným koláčom návštevu dokážeš ohúriť. Matiku pri tom radšej neposmínaj.) Dve tabličky v prvom riadku rozdelené na menšie budú obsahovať po 81 tabličiek a dve tabličky v druhom riadku rozdelené na menšie budú obsahovať po 63 tabličiek.
Ideme kúzliť. Najprv si pozri obrázok:
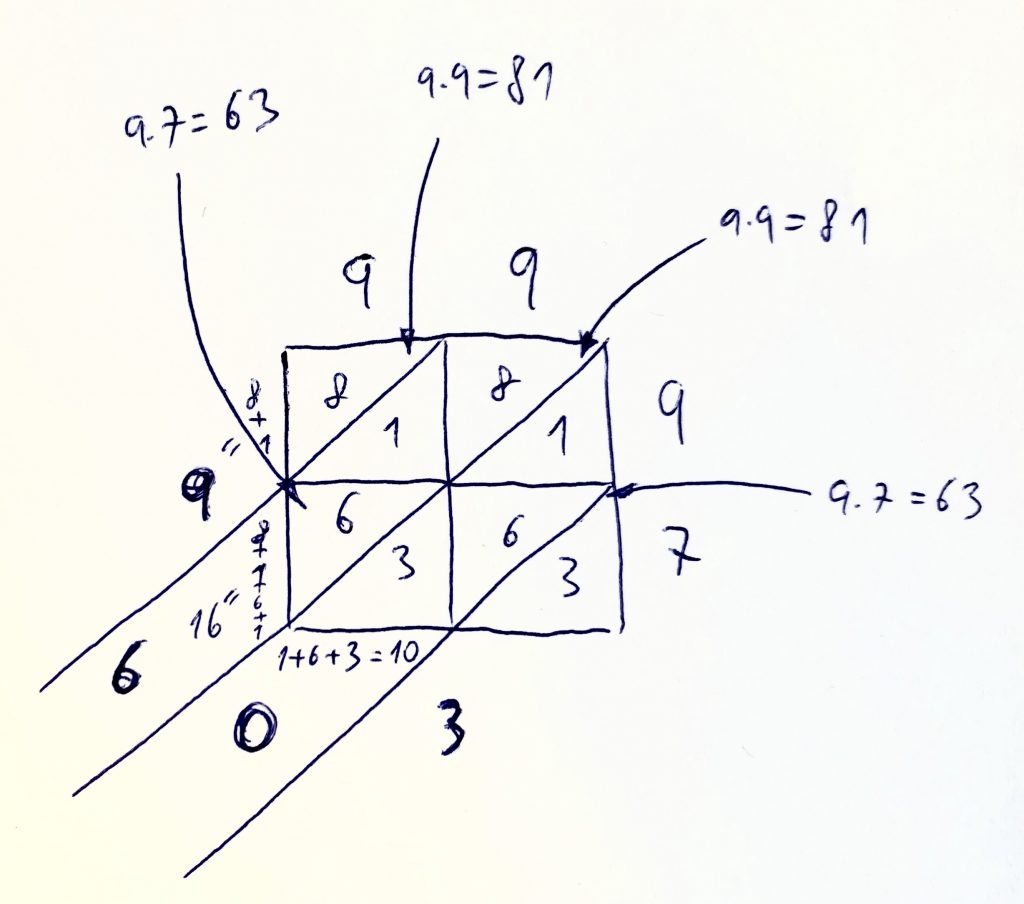
Teraz spočítaj čísla na diagonálach (to sú tie šikmé tunely vzniknuté šikmými rezmi) postupne odzadu. Čiže najskôr získaš číslo 3, potom číslo 10, potom číslo 15, potom číslo 8. Takto odzadu to treba aj upratať.
Nasledujúci odsek čítaj čo najpomalšie, ako sa len dá:
Trojku nechaj tak, z desiatky nechaj nulu, jednotku posuň k číslu 15. Tam dostaneš 16. Z toho čísla nechaj na mieste šestku a jednotku posuň k osmičke. Na prvom mieste tak dostaneš číslo 9.
Čítal si pomaly? Ak nie, ešte raz a sleduj obrázok vyššie.
Výsledok zapíš teraz odpredu ako 9603.
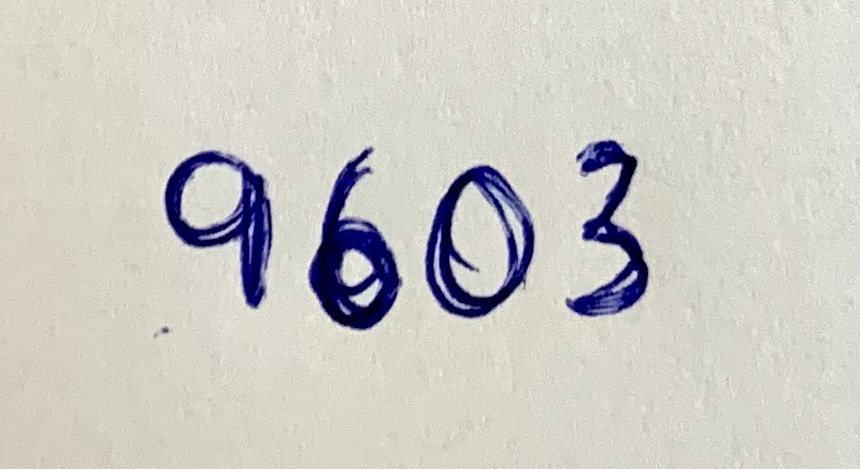
Celý problém násobenia dvoch mierne nechutných čísel si takto rozbiješ na jednoduché násobenie malej násobilky, ktorej výsledky len sčítaš.
Teraz ti odporúčam dať si čokoládu, ale pozor na počet tabličiek (kvôli postave) a na za rohom číhajúceho škrečka.
Dve desatinné čísla
Touto fintou vyrazíš dych nejednému krokodílovi. Za predpokladu, že je rovnako inteligentný, ako ty. Inak to radšej neskúšaj.
Dajme si dve desatinné čísla, ktoré chceš medzi sebou vynásobiť. Hocijaké. Napríklad: 3,14 krát 2,718. Skús to najprv klasickou metódou bez kalkulačky alebo bez PhotoMath (podľa toho, čo máš viac po ruke) a stopni si čas. Nezabudni si dať pri tom čokoládu, budeš ju potrebovať.
Ak máš, mal by si mať výsledok 8,53452.
Teraz na to aplikujme čokoládu a výsledok by mal vyjsť rovnaký. Napíš si obe čísla ako na obrázku nižšie:
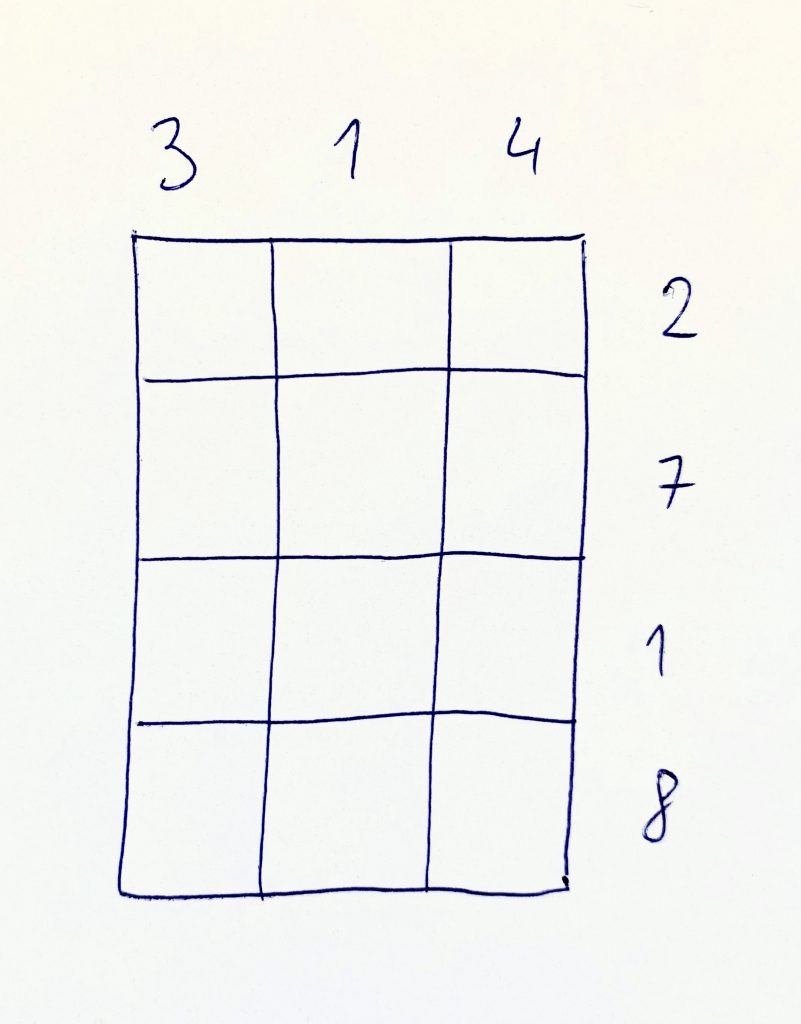
Zámerne nepíšem desatinné čiarky. Nie preto, že by ich zjedol škrečok, ale preto, že ich úloha príde neskôr.
Ak si pozorne sledoval postup násobenia dvoch viacciferných čísel, vieš, čo bude nasledovať. Čokoládu teraz nakrájaj šikmými rezmi podľa diagonálnych čiar, ako na obrázku nižšie.
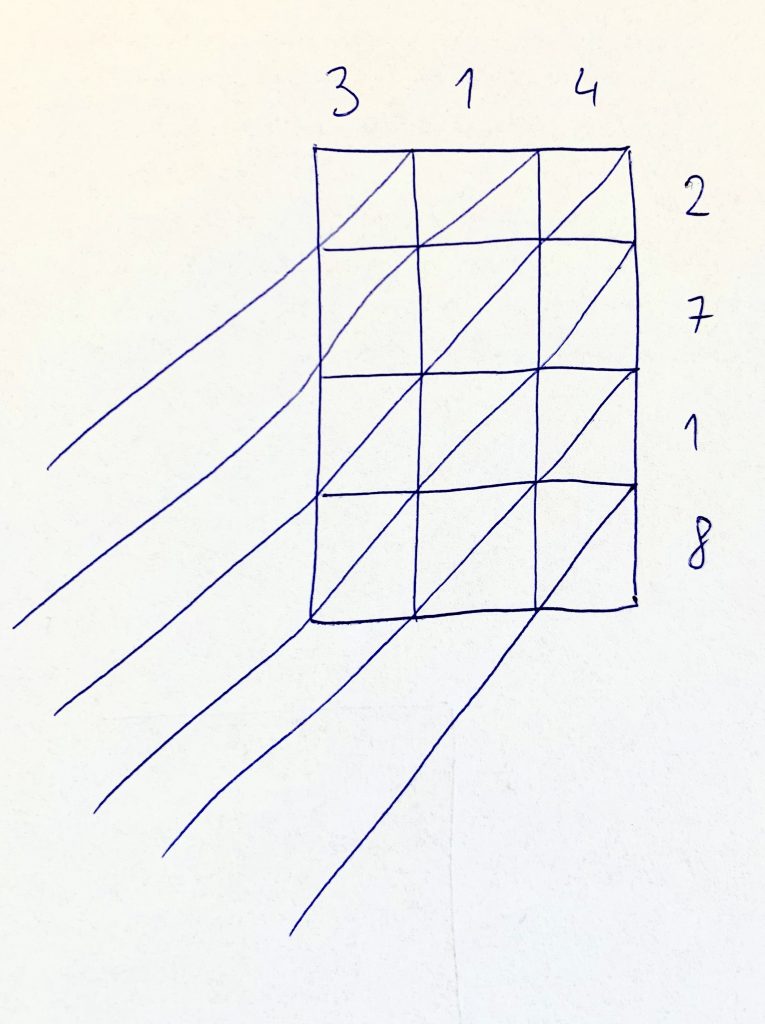
Teraz nasleduje zopakovanie malej násobilky. Najprv kukni obrázok, čo je nižšie a potom čítaj ďalej pod ním. Pozor na škrečka, ktorí to celé sleduje spoza tvojho chrbta, môže kuť pikle.
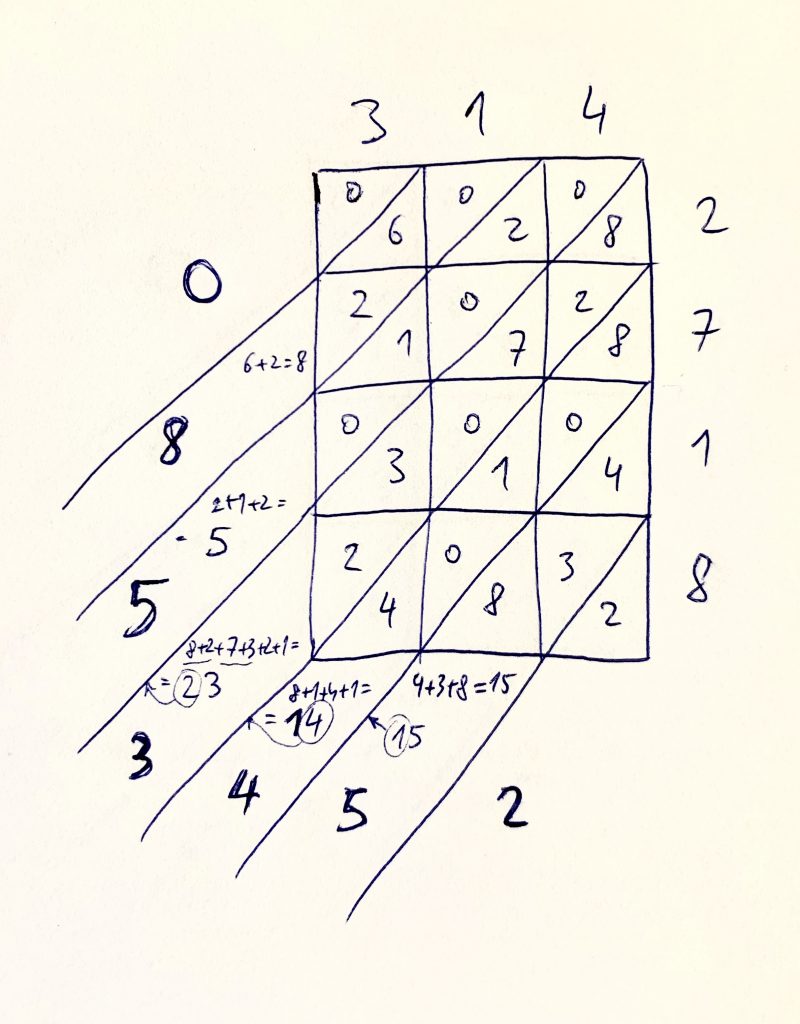
Každá tablička tejto čokolády vytvára novú miničokoládku. Napr. tablička vľavo hore obsahuje výsledok násobenia čísel 3*2, čo je 6. Okolo šikmého rezu v tejto tabličke napíšeme číslo 6 aj s nulou na začiatku v tvare 06. To sa môže. Nula na začiatku nič neznamená, len zníži riziko výpočtovej chyby, rakoviny a srdcovocievnych chorôb. Spočítaj takto čísla v každej tabličke. Prvú cifru výsledku zapíš nad šikmý rez v tabličke, druhú cifru výsledku zapíš pod šikmý rez v tej istej tabličke.
Výsledné čísla spočítame po jednotlivých šikmých tuneloch tak, že ako prvý spočítame najviac pravý tunel. Potom tunel druhý sprava atď. Najprv teda vypočítame číslo 2, potom 5, potom 4, potom 3, potom 5, potom 8, a nakoniec 0. Nezabúdaj na cestujúce cifry, ktoré musíš medzi šikmými tunelmi posúvať, aby bol výsledok presný.
Ak ti to nie je stále jasné, pokukaj obrázky v tomto článku ešte raz, trochu pomalšie, zjedz pri tom čokoládu ? a dávaj pozor na škrečka.
A čo desatinné čiarky?
Do nakrájanej čokolády pridaj 2 kusy desatinných čiarok tak, ako vidíš na nasledujúcom obrázku.
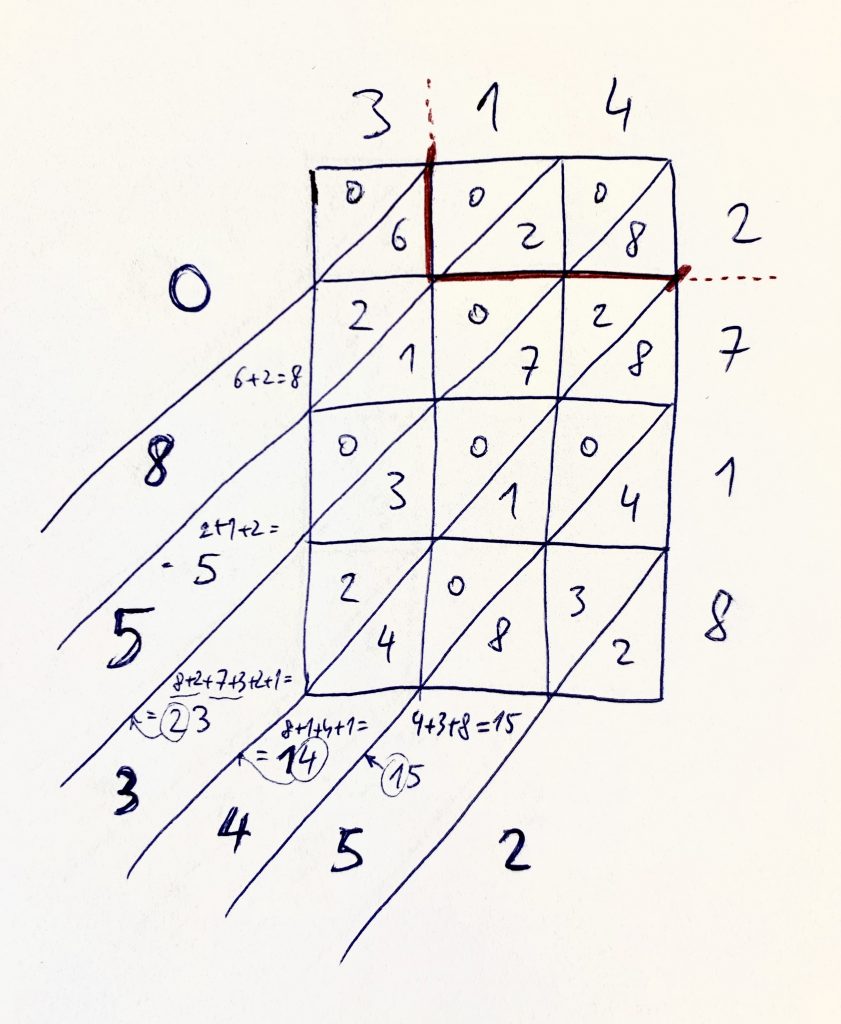
Desatinná čiarka v jednom (3,14) aj druhom čísle (2,718) zvýrazňuje chuť miesta medzi tabličkami, ku ktorým prislúchajú jednotlivé číslice. Čiary, ktoré z čokolády ukazujú na desatinné čiarky, zvýrazni tak, že získaš ich priesečník medzi tabličkami čokolády.
Je všeobecne známe, že priesečníky sú miesta na čokoláde, o ktoré sa nikto nechce deliť. Preto sleduj nasledujúci obrázok a uvidíš, ako sa dve zvýraznené čiary zmenili na jednu, ktorá kopíruje práve jeden šikmý rez čokoládou až k výslednému číslu.
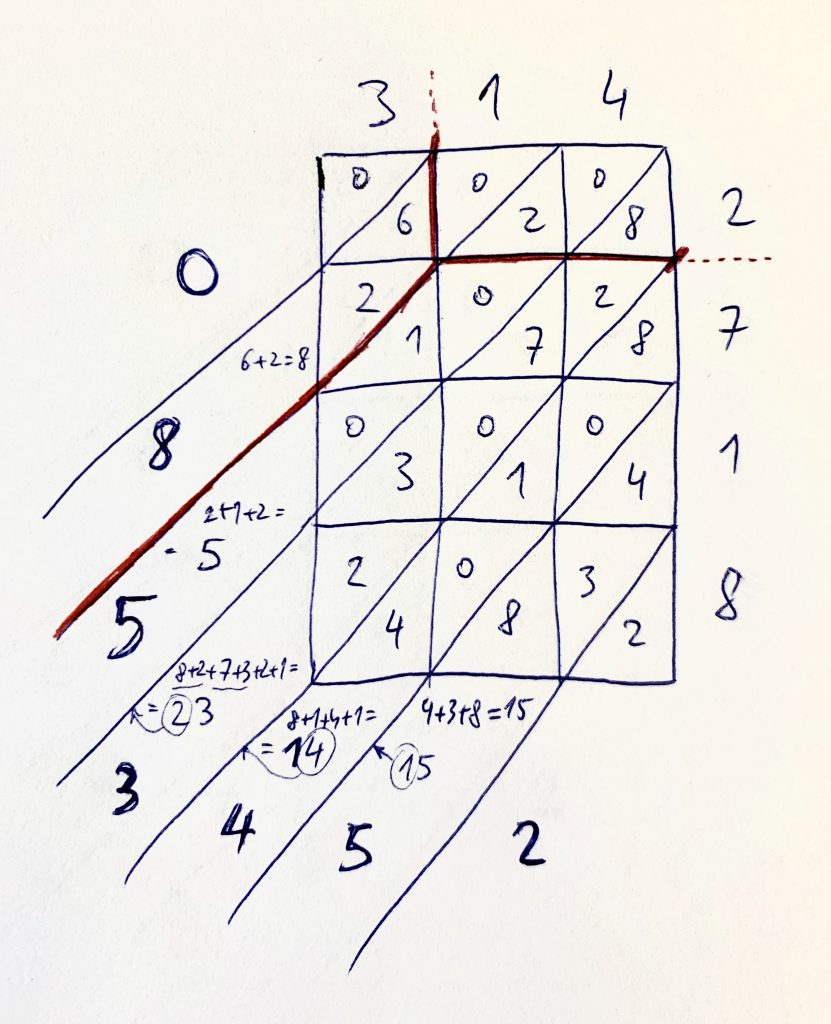
Máme výsledok, čo je číslo 8,53452.
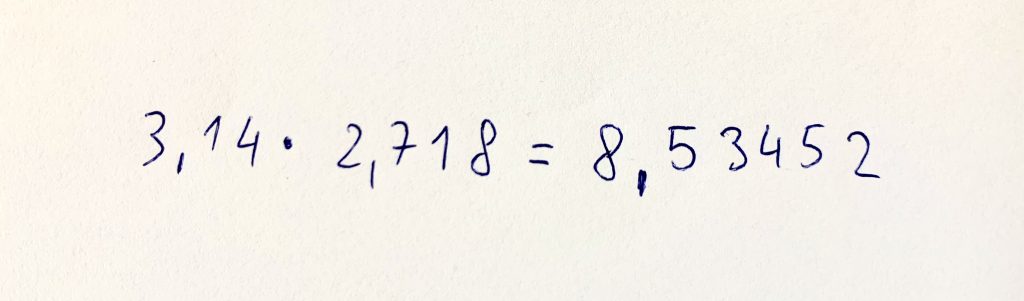
Čokoláda je mocný nástroj v matematike. Ak máš na jednu chuť, daj si, lebo to bude ešte divokejšie.
Čísla zapísané dosť divne
Existujú aj čísla, ktoré sú zapísané dosť zvláštne. Dokonca až tak zvláštne, že nad tým človeku rozum stojí, a škrečkovi koliesko. Pozri obrázok nižšie.
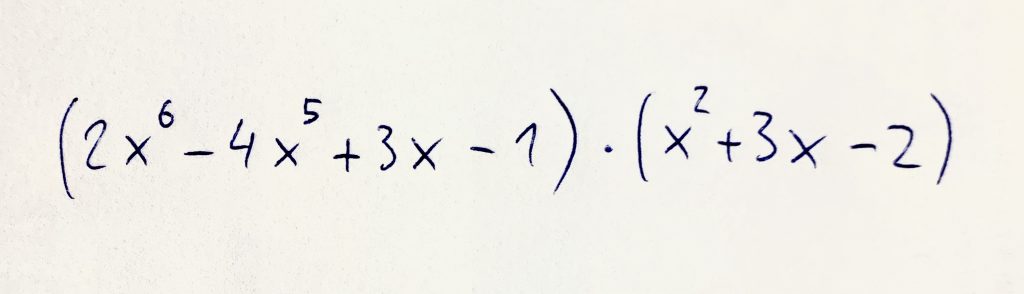
Tieto dve čísla (každá zátvorka vyjadruje jedno číslo) sa nazývajú mnohočleny, lebo majú mnoho členov. Tieto dva mnohočleny chceme vynásobiť. PhotoMath ti síce hneď ukáže výsledok, ale už nezistíš, prečo ten výsledok je taký, aký je. Čokoláda síce nie je zadarmo, ako PhotoMath, ale dokáže to vysvetliť.
Na začiatku sme si povedali, že násobiť môžeš medzi sebou dve ľubovoľné čísla alebo veci. Rovnako je nutné chápať, že každý z mnohočlenov v uvedenom zápise je jedno číslo. Tieto čísla nazvime úsečkami. A čo sa stane, ak vynásobíme medzi sebou dve úsečky? Vypočítame obsah nejakého útvaru. V tomto našom prípade bude tým útvarom čokoláda. Chutné, že?
Označme si každý mnohočlen ako úsečku.
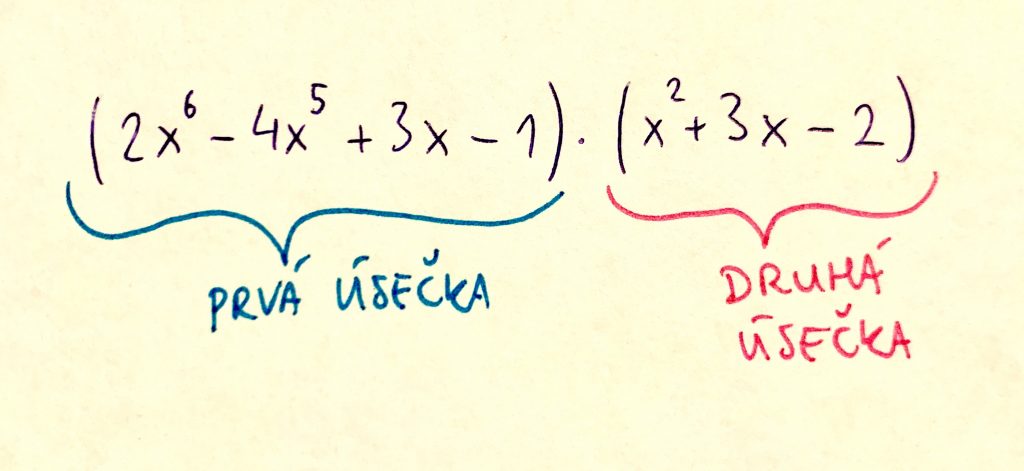
Teraz si to predstav ako násobok „úsečka krát úsečka“, čo je v podstate obsah nejakého obdĺžnika. Ten obdĺžnik nazvime čokoláda.
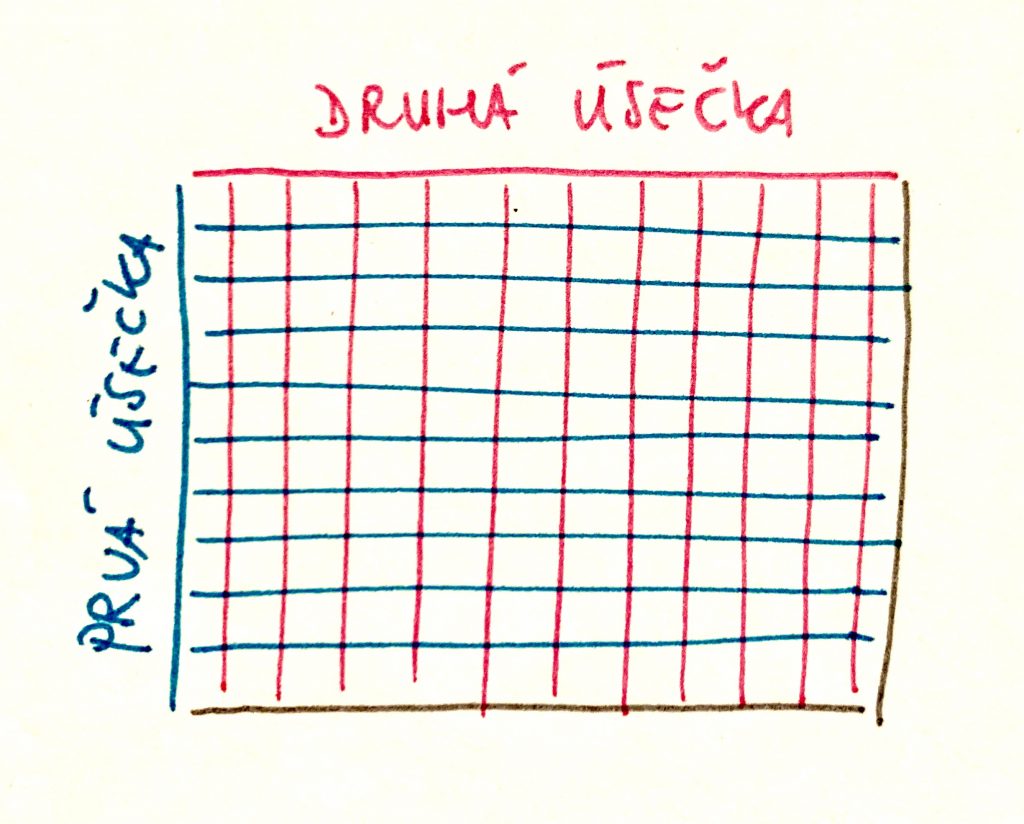
Prvú aj druhú úsečku prepíšme pomocou oboch mnohočlenov takto:
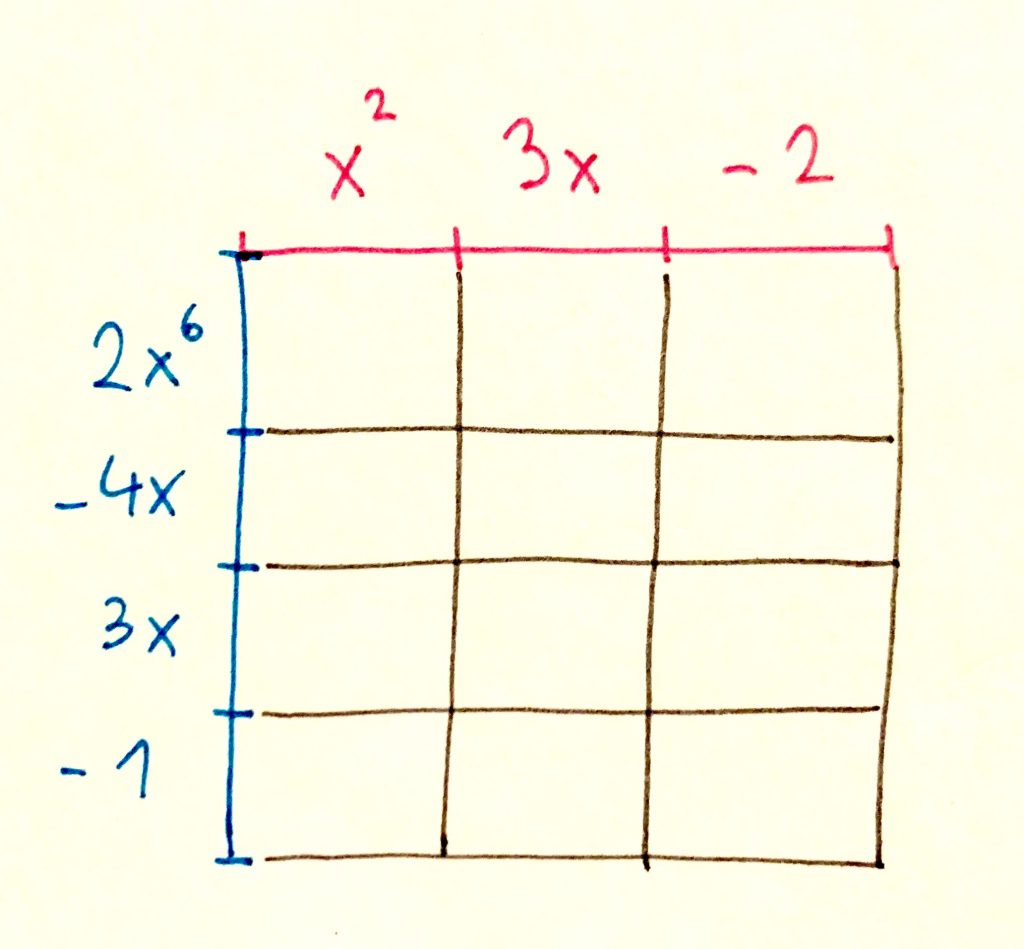
Dĺžku úsečiek som rozpísal pomocou členov mnohočlenov tak, ako sú zapísané. Pri tomto prepise nesmieš zabudnúť na znamienka mínus. Matematika v tomto prípade umožňuje aj kúzla vo forme úsečiek so zápornou dĺžkou (mínus jedna, mínus dva, mínus štyri ix), čo by v realite nebolo možné. Vieš si predstaviť čokoládu s mínus tromi tabličkami na šírku? Ja nie, možno len prejedený škrečok.
V tejto chvíli potrebuješ trochu poznať počítanie s mocninami, avšak nie je to až tak nutná podmienka, lebo čím viac čokolád zješ, tým viac budeš vedieť s mocninami počítať. A keď to nebude fungovať, predsalen klikni sem a zaskroluj dole. Alebo môžeš kuk aj na Wikipediu. Je pravda, že existujú učitelia, ktorí webové zdroje zatracujú ako zdroj chýb, ale keď si všetko overíš aspoň z dvoch rôznych zdrojov, ku chybe sa dopracuješ s minimálnou pravdepodobnosťou. Aj tento článok bude patriť do množiny zatracovaných zdrojov 😉 a pri tom zvyšovať pravdepodobnosť tvojho úspechu pri maturite alebo na nejakej písomke.
Pozri čokoládu na obrázku nižšie a zamysli sa nad tým, čo sa v jej tabličkách odohralo.
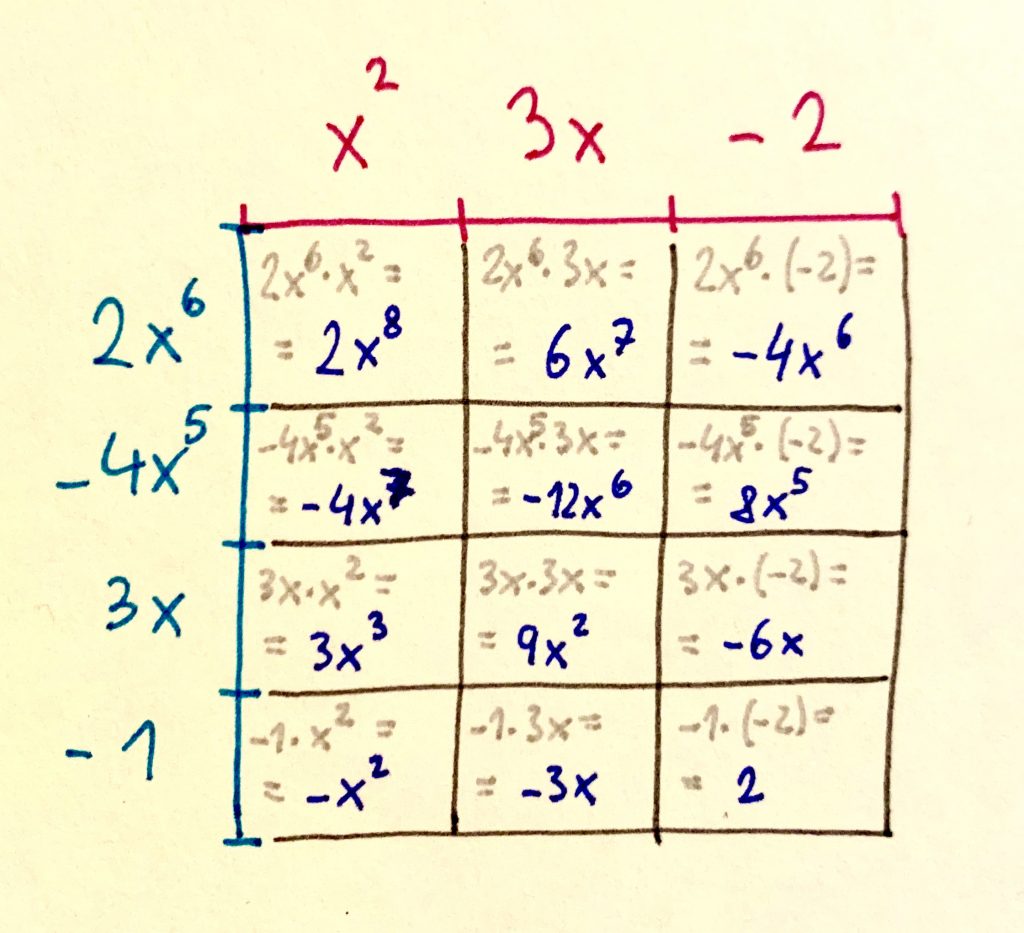
Výsledok súčinu dvoch na začiatku uvedených mnohočlenov bude súčet tabličiek výslednej čokolády:
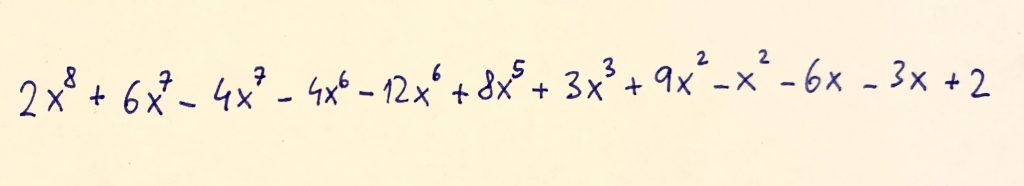
Ixká s rovnakým exponentom sčítame spolu ako jabĺčka. Ixk na siedmu s iným ixk na siedmu atď. Výsledok bude potom tento:
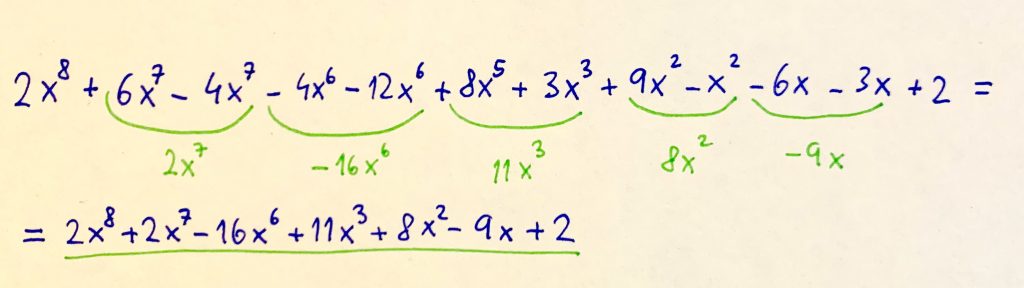
Pozri sa ešte raz na celý proces v jednej kôpke.

Ja viem, výsledok moc krásny nie je oproti zadaniu, ale čokoláda ilustruje metódu tohto násobenia tak, aby ho osladila. Niekedy sa totiž stane, že celý výraz sa dá ešte viac zjednodušiť, ale to už nie je predmetom tejto úvahy.
Tak si to vyskúšaj práve pomocou metódy čokoláda:
\[(4x^3+5x^2-2x-12)*(2x^4-7x^2+2)\]A pozor na postavu…

Pridaj komentár