Značka: funkcia
-
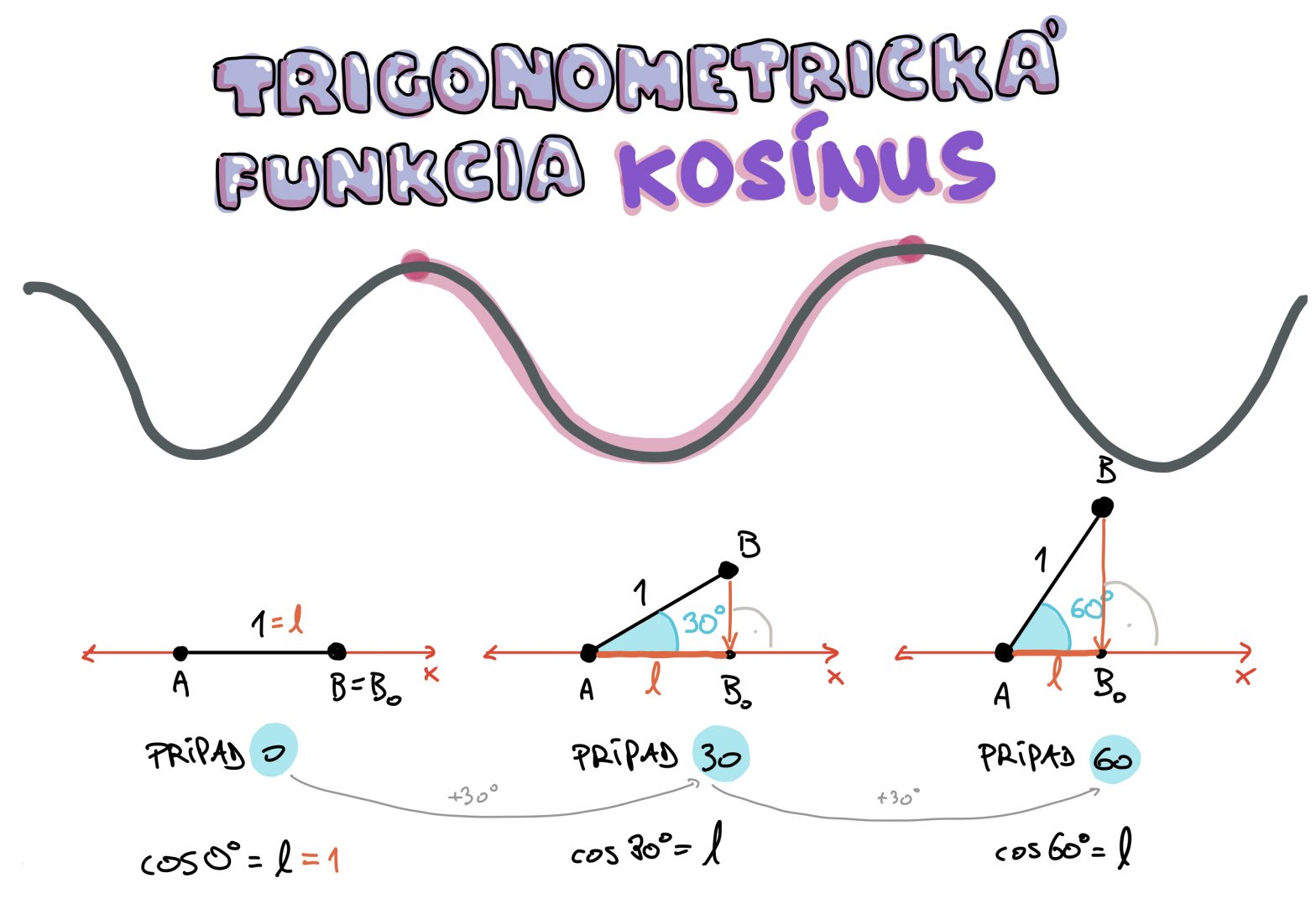
Trigonometrická funkcia kosínus
Kosínus je funkcia, ktorá je súrodencom funkcie sínus. Je k tej prilepená v tesnom závese o pravý uhol. Tak sleduj, a uč sa!
-

Logaritmická funkcia
Logaritmická zmena nejakého vzoru (patternu) je v zásade spomaľujúca. Čím dlhšie sa na zmenu pozeráš, tým pomalšie sa mení a stále spomaľuje. V tejto sérii videí si môžeš pozrieť, ako získať z pozorovania takej zmeny všeobecný vzorec, nejaké dáta a nakoniec graf. Vlastnosti logaritmickej funkcie z toho všetkého vyplynú samé.
-

Exponenciálna funkcia
Exponenciálna funkcia je vzťah, ktorý popisuje postupné násobenie čísla samého so sebou v časopriestore. Napríklad šírenie vírusov prebieha exponenciálne, alebo rozširovanie priestoru o nové dimenzie prebieha exponenciálne. Viac sa dozvieš v sérii videí, kde vyskúmame všeobecný vzorec, vytvoríme graf zmeny takéhoto tvaru a popíšeme si vlastnosti funkcie, ktorá toto popisuje.
-
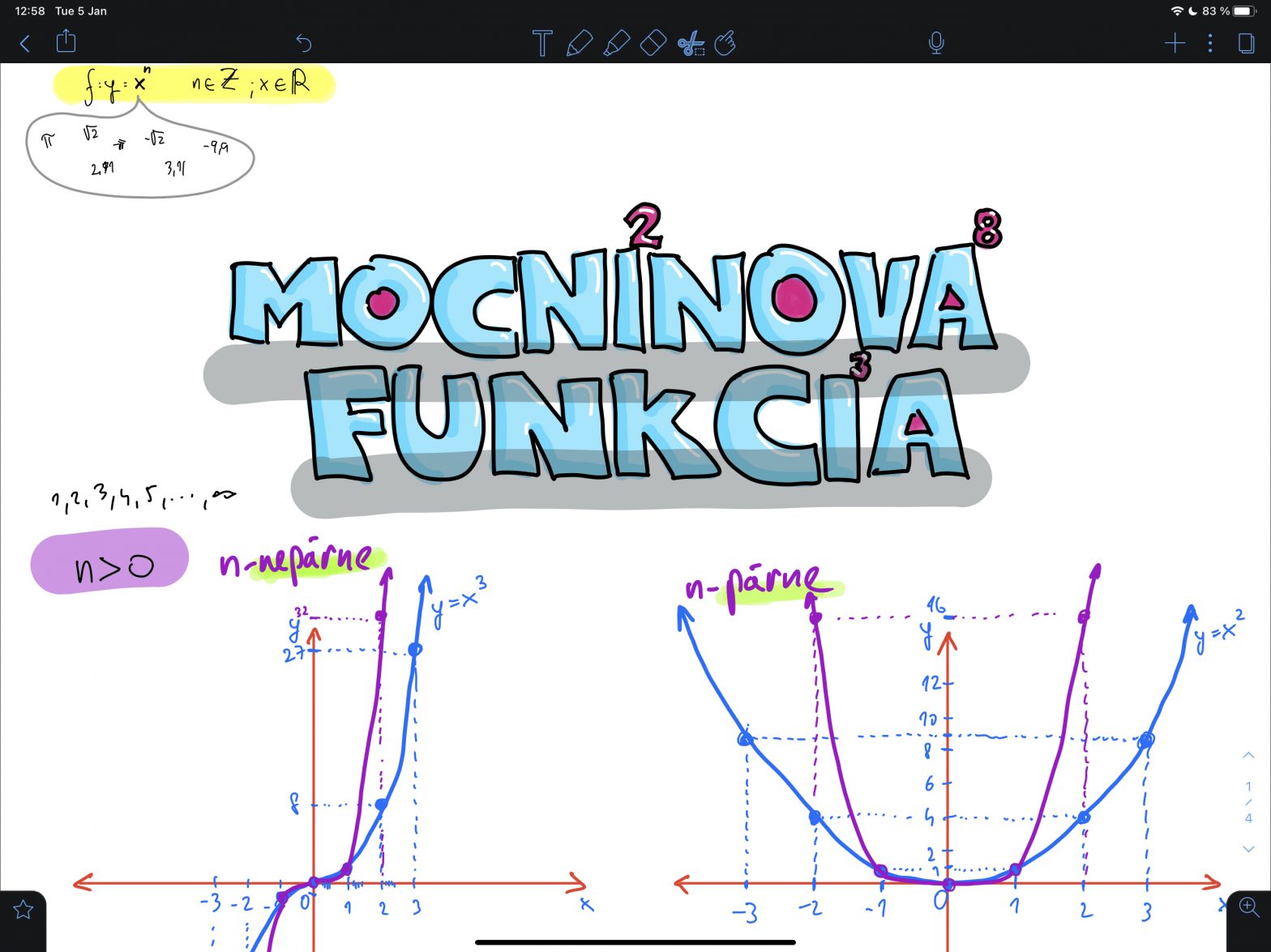
Mocninová funkcia
Mocninová funkcia je také čudo medzi funkciami, pretože už nebolo názvov na pomenovanie všetkých druhov funkcií, tak boli pomenované všeobecným názvom mocninové. V zásade môžeme kľudne prehlásiť, že mocninovými funkciami sú všetky druhy funkcií, ktoré poznáme a narábajú s čistou hodnotou x. Ako to myslím? No tak, že funkcie ako sin(x), log(x), e^x nie sú…
-

Lineárne lomená funkcia
Lineárne lomená funkcia sa volá preto tak, lebo je to podiel dvoch lineárnych funkcií, napríklad: V tejto sérii sa pozrieme na jeden prípad zmeny tvaru, ktorá sa dá popísať práve takto. Inými slovami sa dá povedať, že lineárne lomená funkcia je nepriama úmernosť posunutá o nejakú hodnotu horizontálne a o nejakú hodnotu vertikálne. Popíšeme si…
-
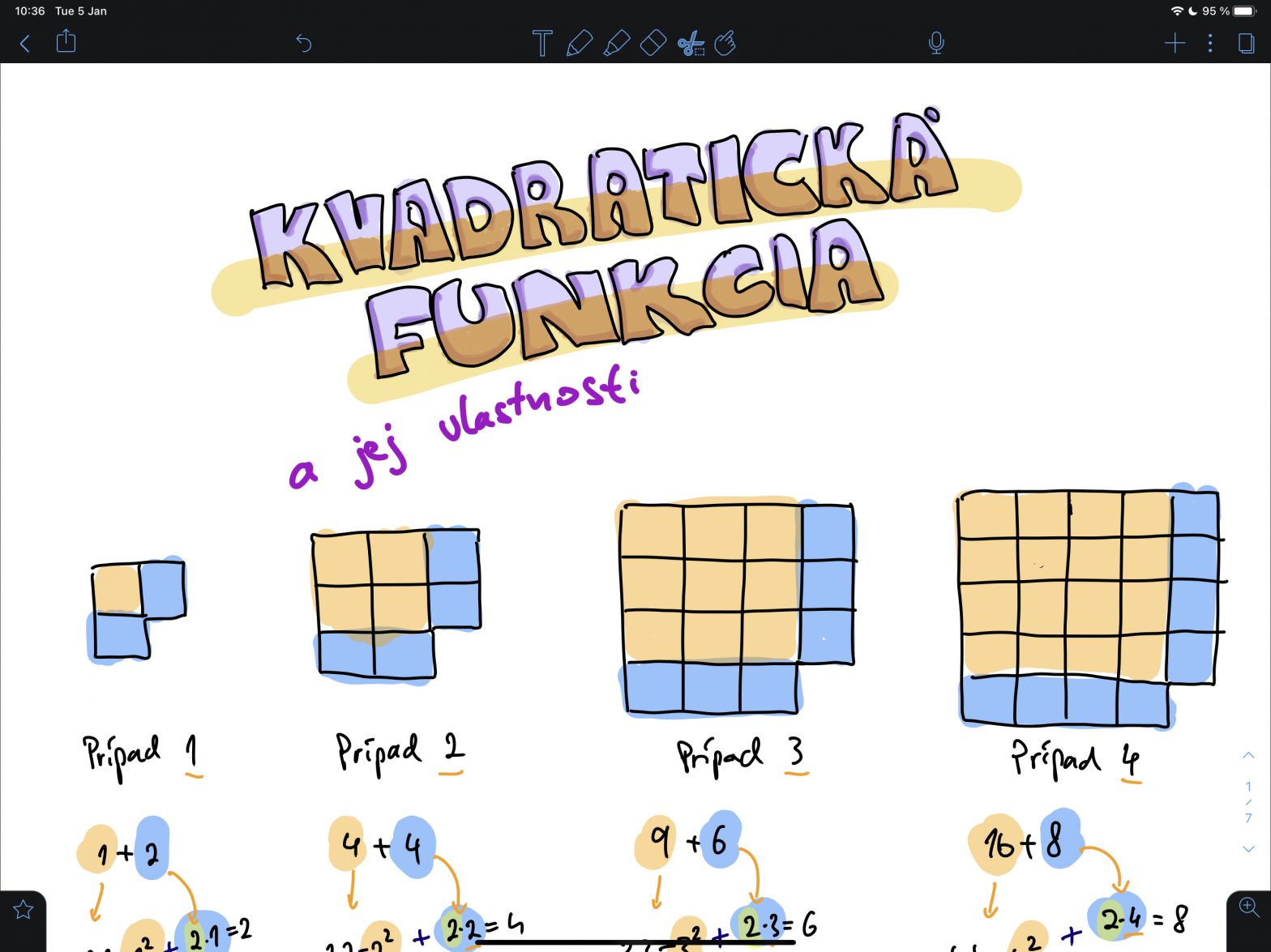
Kvadratická funkcia
Kvadratická funkcia bola popísaná na základe skúmania tvarov, ktoré sa menia s druhou mocninou. Napríklad zmena plochy dačoho. Či už plochy štvorca vzhľadom na dĺžku strany, plochy kruhu vzhľadom na polomer, alebo hodnoty y vzhľadom ku hodnote x^2. V tejto sérii sa pozrieme na pár zaujímavých vlastností kvadratickej funkcie, ako je jej priebeh (bez derivácie),…
-
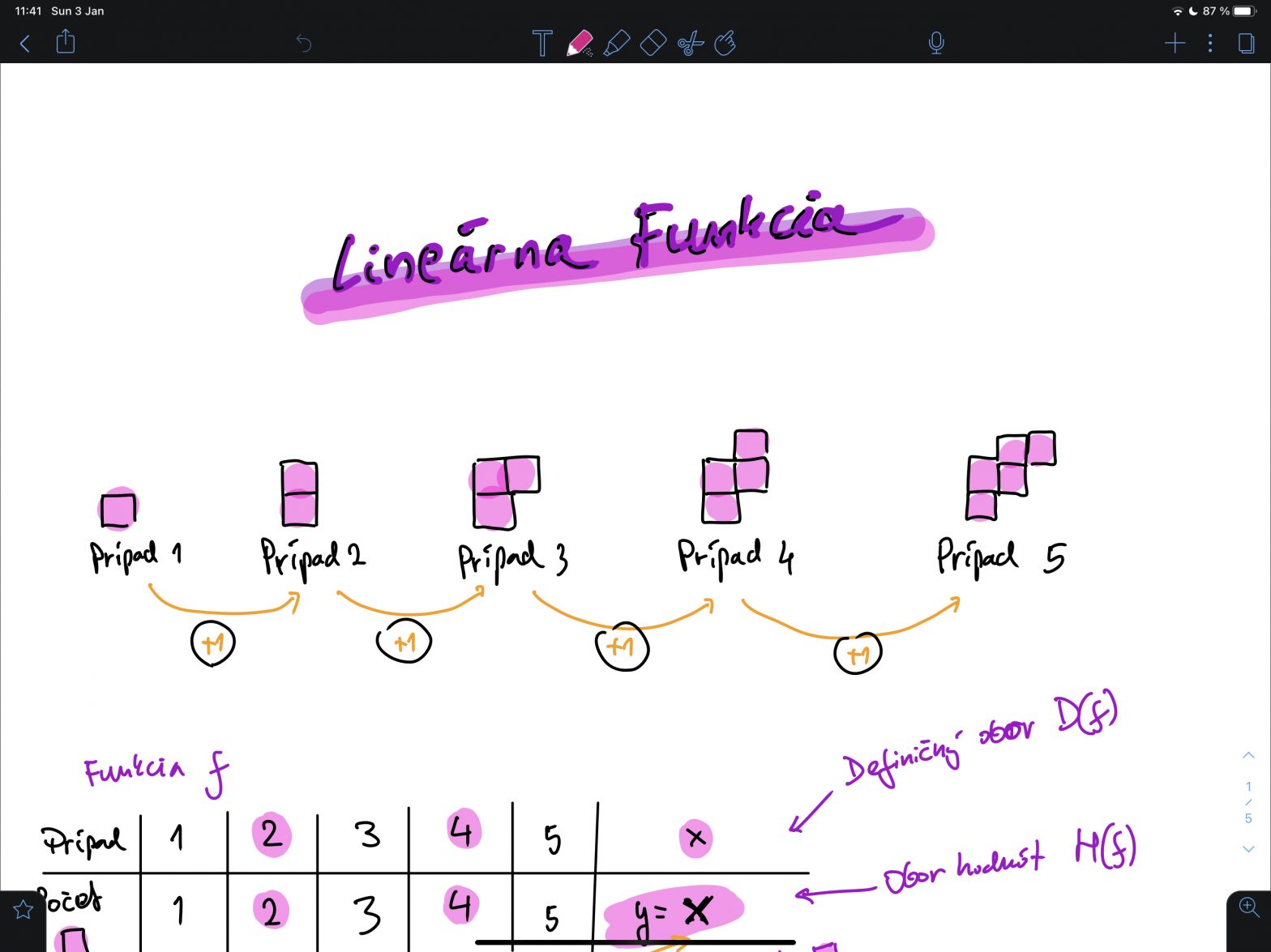
Lineárna funkcia
Na lineárnu funkciu sa pozrieme z pohľadu zmeny tvaru v časopriestore tak, aby bolo zrejmé, ako vzniká vzorec, čo popisuje graf a aké sú jej vlastnosti. Pozrieme sa na zúbok rastúcej, klesajúcej aj konštantnej zmeny tvaru.
-
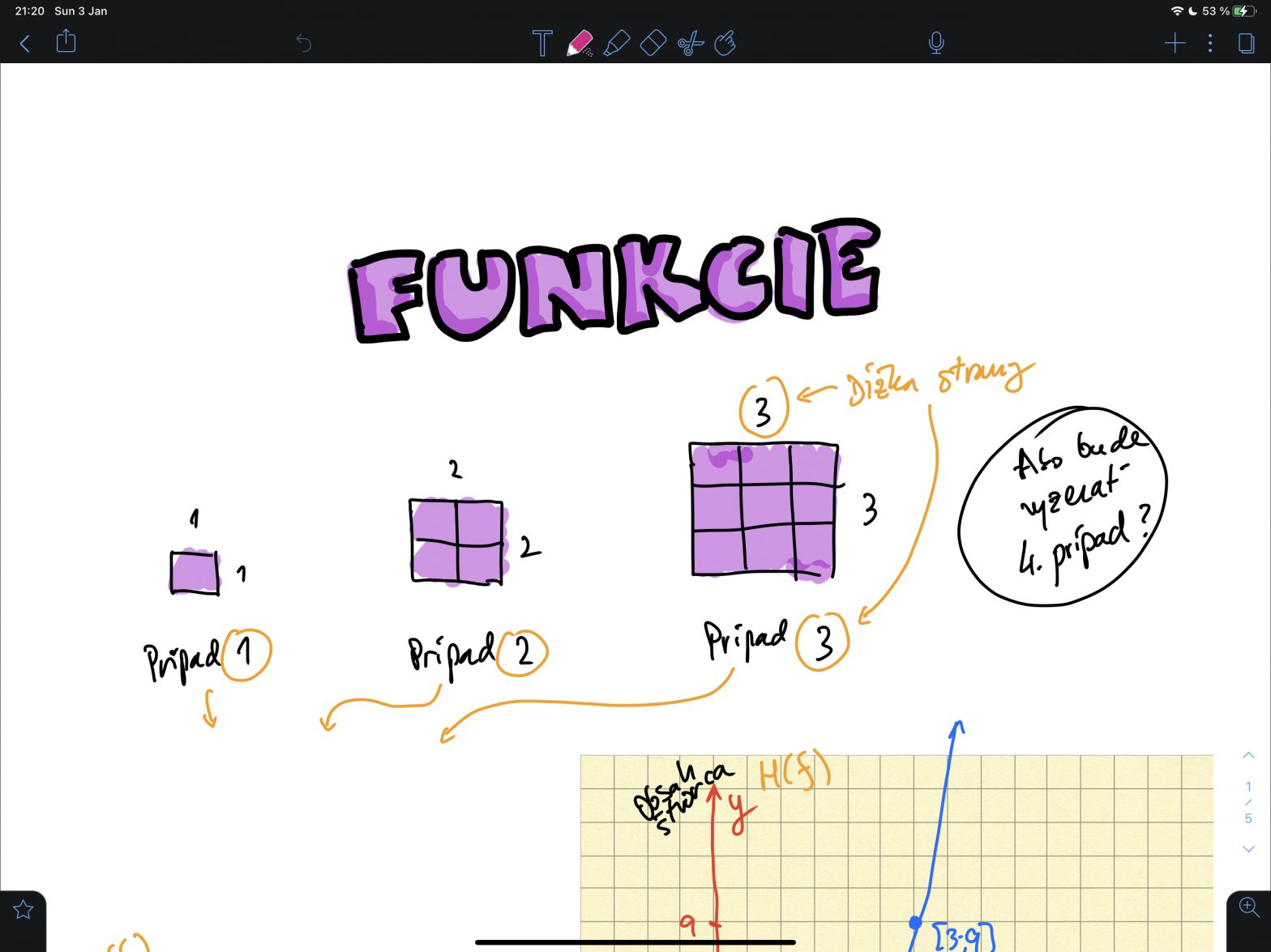
Funkcie – vzťahy v matematike
Funkcia sa dá vyjadriť zmenou tvaru, ktorý sa mení v priestoročase vzhľadom na stavy pozorovateľa. Natočil som o nich sériu popisných videí, tak pokukaj, aby si chápal/a funkcie v zmysle matematiky. Daj mi vedieť, ak pomohlo, do komentár pod konkrétne video, čo bolo pre teba najviac prínosné. Ďakujem ??.